高校数学の絶対値の問題は、グラフでイメージしよう。(その5)

読了時間: 約4分46秒
[mathjax]
自宅のパソコンでブログ記事を書いていたはずが、
突然不思議な世界に迷い込み、
高校生?恐竜、ディノさんと出会ってしまった私。
ディノさんは、絶対値の問題の解き方を教えてくれたら、ひらけた場所までの案内をしてくれると言いますが・・・
さて、今日の問題の「解法」で、ディノさんは私を「解放」してくれるのでしょうか。
![]()

ディノ
いや~、肉、うまかったなぁ。

Lukia
ぞ、ぞうでづね・・・

ディノ
やっぱ、「いきなり焼肉」、うまいだろ?

Lukia
なんですか、そのフューチャリングした店名はっ。
怒られますよ?
というか、いつもあんなサイズのお肉、食べてるんですか?
怒られますよ?
というか、いつもあんなサイズのお肉、食べてるんですか?

ディノ
若いから食っとかないとな。(笑)
タンパク質取らないと、頭がはたらかねぇんだぞ。
というわけで、今、オレの頭、調子いいぞ。
一問いっとくか?
タンパク質取らないと、頭がはたらかねぇんだぞ。
というわけで、今、オレの頭、調子いいぞ。
一問いっとくか?

Lukia
うひぃ・・・
ひとまず、胃腸薬ください・・・
ひとまず、胃腸薬ください・・・
私の胃のことなんておかまいなし。
ディノさんは、人の話を聞かずに、問題を見せました。
問題
$$\Large \color{blue}{\vert 2x \vert}+\color{red}{\vert x-2 \vert}=6$$
簡単な図を描こう。
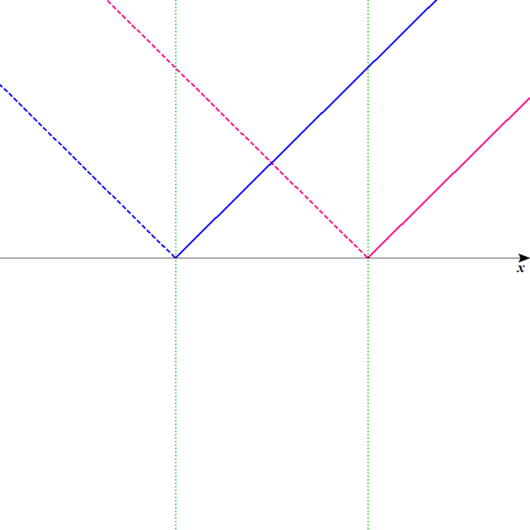

Lukia
前回と同様、式の中に絶対値が2つ存在しているので、
上のような簡単な図を描いて、それを用いて問題を解いていきます。
上のような簡単な図を描いて、それを用いて問題を解いていきます。

ディノ
おう。
そして、グラフの下が計算スペースになるから、あけとくんだったよな。
そして、グラフの下が計算スペースになるから、あけとくんだったよな。

Lukia
そうですね。
範囲を設定しよう。

Lukia
絶対値が絡む問題は、まずは範囲がどうなっているのかを把握してやる必要があります。
というわけで、青と赤のV字の起点、つまり、\(x\)軸と交わっているのは\(x\)がいくつのときかを求めていきましょう。
というわけで、青と赤のV字の起点、つまり、\(x\)軸と交わっているのは\(x\)がいくつのときかを求めていきましょう。

ディノ
オレ、コレわかる。
\(\color{blue}{\vert 2x \vert=0}\)となるのは、
\(x=\color{blue}{0}\)のときで、
\(\color{red}{\vert x-2 \vert=0}\)となるのは、
\(x=\color{red}{2}\)のときだ。
\(\color{blue}{\vert 2x \vert=0}\)となるのは、
\(x=\color{blue}{0}\)のときで、
\(\color{red}{\vert x-2 \vert=0}\)となるのは、
\(x=\color{red}{2}\)のときだ。

Lukia
そうですね。
つまり、これによって、図の緑の点線によって3分割されている範囲が、
左が、\(x \leq 0\)
真ん中が、\(0 \leq x \leq 2\)
右が、\(2 \leq x\)となりますね。
図は以下のようになりますね。
つまり、これによって、図の緑の点線によって3分割されている範囲が、
左が、\(x \leq 0\)
真ん中が、\(0 \leq x \leq 2\)
右が、\(2 \leq x\)となりますね。
図は以下のようになりますね。
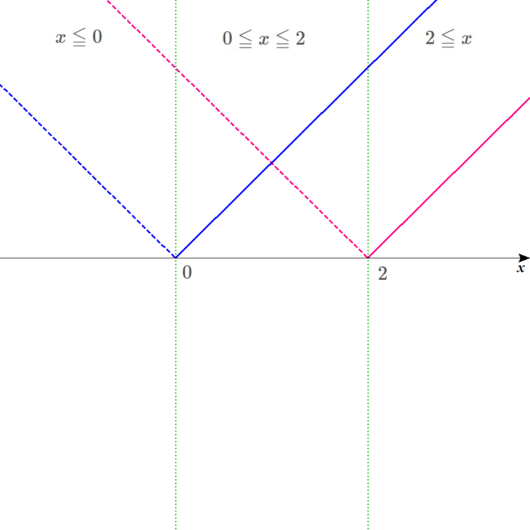
範囲ごとに式を書き込んでいく。

ディノ
範囲がわかると、式の正負も考えやすいよな。

Lukia
そうですね。
・・・ディノさん、図に式を書き込んでもらえますか?
私、今しゃべるの無理です・・・。
・・・ディノさん、図に式を書き込んでもらえますか?
私、今しゃべるの無理です・・・。

ディノ
おう、いいぞ。
まず、青いほうから片付けるかな。
\(\color{blue}{y=\vert 2x \vert}\)は、
\(y=\color{blue}{-2x}\) \(\left( \color{blue}{x \leq 0} のとき\right)\)
\(y=\color{blue}{2x}\) \(\left( \color{blue}{0 \leq x} のとき\right)\)だ。
まず、青いほうから片付けるかな。
\(\color{blue}{y=\vert 2x \vert}\)は、
\(y=\color{blue}{-2x}\) \(\left( \color{blue}{x \leq 0} のとき\right)\)
\(y=\color{blue}{2x}\) \(\left( \color{blue}{0 \leq x} のとき\right)\)だ。

Lukia
つぶぅけて・・・

ディノ
\(\color{red}{y=\vert x-2 \vert}\)は、
\(y=\color{red}{-x+2}\) \(\left( \color{red}{x \leq 2} のとき\right)\)
\(y=\color{red}{x-2}\) \(\left( \color{red}{2 \leq x} のとき\right)\)だ。
\(y=\color{red}{-x+2}\) \(\left( \color{red}{x \leq 2} のとき\right)\)
\(y=\color{red}{x-2}\) \(\left( \color{red}{2 \leq x} のとき\right)\)だ。

Lukia
わかった式を図に書き込むと、以下のようになりますね。
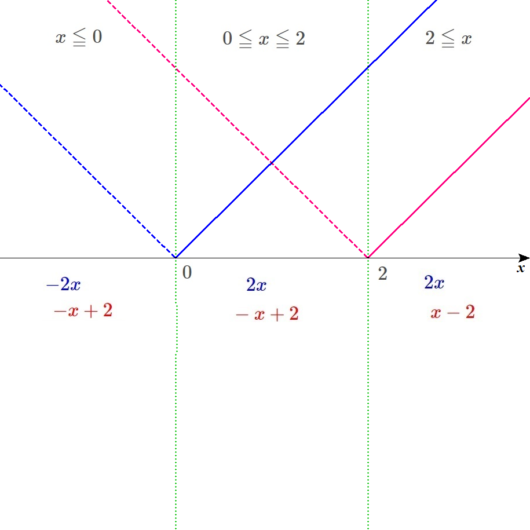
筆算する。

Lukia
ここまでできたら、今回の問題は、2つの絶対値が+(プラス)でつながっているので、
たし算の筆算をします。
たし算の筆算をします。

ディノ
左が、\(-3x+2\)
真ん中が、\(x+2\)
右が \(3x-2\)になるよな。
真ん中が、\(x+2\)
右が \(3x-2\)になるよな。

Lukia
はい。
図には、このように書き込めばよいですね。
図には、このように書き込めばよいですね。
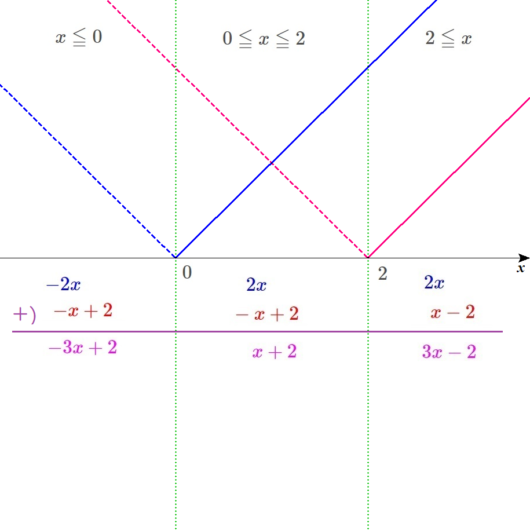
グラフを描くとこうなる。

Lukia
さて、絶対値をはずして、それぞれの範囲ごとに筆算をした結果をグラフにすると、
以下のような図になります。
以下のような図になります。
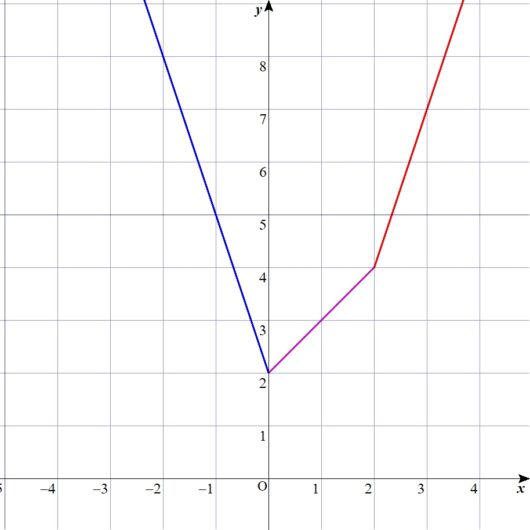

ディノ
なんか、オレの歯みたいな形してんな。
方程式を解く。

Lukia
ここまでは、左辺の式を変形してきました。
いよいよ、=6 をつけて、方程式を解いてみましょう。
いよいよ、=6 をつけて、方程式を解いてみましょう。

ディノ
ってことは、
左から、\(-3x+2=6\)
\(x+2=6\)
\(3x-2=6\)を解けばいいってことだな。
左から、\(-3x+2=6\)
\(x+2=6\)
\(3x-2=6\)を解けばいいってことだな。

Lukia
そうですね。

ディノ
ということは、
左の範囲は、\(x=-\frac{4}{3}\)
真ん中の範囲は、\(x=4\)
右の範囲は、\(x=\frac{8}{3}\)だな。
左の範囲は、\(x=-\frac{4}{3}\)
真ん中の範囲は、\(x=4\)
右の範囲は、\(x=\frac{8}{3}\)だな。
範囲を比較して答えを出す。

Lukia
方程式の解を、実際に\(x\)軸上に置いてみましょう。
左の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
真ん中の範囲の解は、紫の四角で囲み、\(x\)軸には、紫の矢印で、だいたいの位置を示します。
右の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。
左の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
真ん中の範囲の解は、紫の四角で囲み、\(x\)軸には、紫の矢印で、だいたいの位置を示します。
右の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。
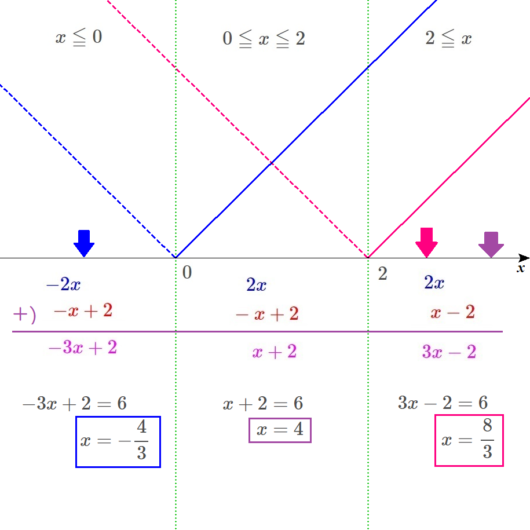

ディノ
あれっ、真ん中の紫の矢印が、右の範囲にあるぞ。
それどころか、赤い矢印よりも右にあるぞ!
それどころか、赤い矢印よりも右にあるぞ!

Lukia
そうです。
つまり、真ん中の範囲で出た答えの4は、不適ということになりますね。
ちなみに、さっきのディノさんの歯みたいなグラフでも、確かめてみましょう。
つまり、真ん中の範囲で出た答えの4は、不適ということになりますね。
ちなみに、さっきのディノさんの歯みたいなグラフでも、確かめてみましょう。
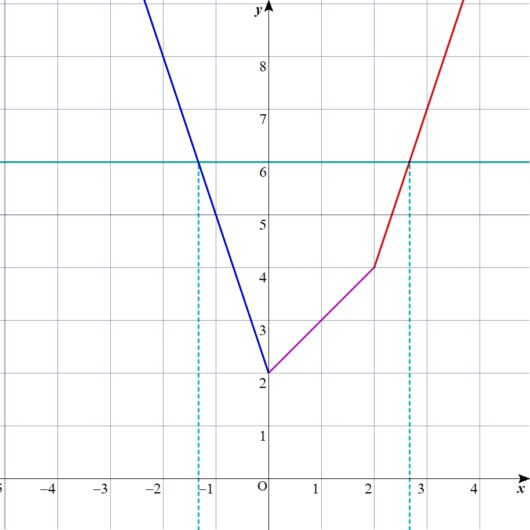

ディノ
たしかに。紫の線を右側に伸ばしていけば、\(x=4\)のとき、\(y=6\)の線と交わるけど、
紫の線は、存在しないからなぁ。
紫の線は、存在しないからなぁ。
こたえ
$$\Large \vert 2x\vert+\vert x-2 \vert=6$$
$$\Large x=-\frac{4}{3} , x=\frac{8}{3}$$
「解放」なるか?

ディノ
いや~、この問題も解けたぞ!
この調子なら、宿題もちゃっちゃと終わりそうだな。
この調子なら、宿題もちゃっちゃと終わりそうだな。

Lukia
よかったです・・・
あ、なんか明るい場所に出てきましたね。
(へぇ、恐竜の世界にも、大通りがあるのか・・・)
じゃ、私は、このへんで。
ディノさん、数学、がんばってくださいねっ。
あ、なんか明るい場所に出てきましたね。
(へぇ、恐竜の世界にも、大通りがあるのか・・・)
じゃ、私は、このへんで。
ディノさん、数学、がんばってくださいねっ。

ディノ
何言ってんだよ。
オマエ、道わかんねぇだろ?
オレが、「ひらけた場所」まで案内するって決めたんだから、ついてくりゃいいんだよ。
それに、まだ問題残ってるぞ?
オマエ、道わかんねぇだろ?
オレが、「ひらけた場所」まで案内するって決めたんだから、ついてくりゃいいんだよ。
それに、まだ問題残ってるぞ?

Lukia
いや、それは、ディノさんの宿題ですから、
ディノさんがやらないと・・・
それに、もうやり方わかったでしょ?
ディノさんがやらないと・・・
それに、もうやり方わかったでしょ?

ディノ
いやっ、まだだッ!
それに、ここで単独行動すると、危ないぞ。
ここらへん、ティラン先輩の縄張りだからな。
それに、ここで単独行動すると、危ないぞ。
ここらへん、ティラン先輩の縄張りだからな。

Lukia
ティラン先輩?
・・・もしかして、ティラノサウルスの?
・・・もしかして、ティラノサウルスの?

ディノ
そうだ。ティラン先輩は、パンクでファンキーでロックなんだぞ!

Lukia
なんとなく、怖いってより、楽しそうな方のようですが・・・。

ディノ
ふん。とりあえず、まだだめだっ。
あ、それより、数学解いたら、腹減ったな。
デザートどうだ?
スイーツ食いに行こうぜ♪
あ、それより、数学解いたら、腹減ったな。
デザートどうだ?
スイーツ食いに行こうぜ♪

Lukia
さっき、頭働かすにはタンパク質って言ってたじゃないですか。
言ってることめちゃくちゃですよ・・・
言ってることめちゃくちゃですよ・・・

ディノ
よし、今日はパフェだな。

意外にもスイーツ男子?なディノさんでした。
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません