高校数学の絶対値の問題は、グラフでイメージしよう。(その4)

[mathjax]
プロローグ

2018年9月6日。
私は、自宅のパソコンでブログ記事を書いていたはずでした。
いつもお世話になっているPixabay(ピクサベイ)で、記事に使えそうな写真を探していたら、
突然、パソコンの画面が光りました。
あまりにまばゆいので、目を閉じ、目のあたりを手で覆いました。
そのうちに、まぶしい光はおさまりました。
おそるおそる目を開けて、また驚きました。

自宅にいたはずなのに、森の中にいたのです!
途方に暮れましたが、情報を得るため、ひらけた場所を探して歩くことにしました。
不安を振り払うようにひたすら歩くことに集中していましたが、背後から、ザザッ、ザザッという音は聞こえてきます。
(やだなぁ。クマとかだったらどうしよう。)
いえいえ、クマより恐ろしいかもしれません。
意を決してふりかえったら・・・
ぎゃぁあああああああ~~~~!!!
アロサウルスがいたのです。
有名な恐竜の映画でしたら、もっぱら人間は驚かされるわ、襲われるわ、食べられるわですが、
それとは勝手が違うようでした。
こっちも驚きましたが、同様にむこうも驚いたようです。
ギィエエエエエエエーーーー!!!
恐竜だけに、声も大きく、森に住むほかのいきものがその声に驚いて、ザワザワと森の葉っぱの音を立てて逃げました。

Lukia
私は、食べてもおいしい歳じゃないからッ!

アロサウルス

Lukia
ん?もしかして、着ぐるみ?

アロサウルス

Lukia
というか、ここはどこですか?
私、さっきまで家にいたはずなのに、こんな場所にいて・・・。
よかったら、ひらけた場所まで案内してもらえませんか?

アロサウルス

Lukia

アロサウルス
よし、ことと次第によっちゃ、案内してやらないでもない。

Lukia
うわぁ~~~、助かりますぅ~。
ありがとうございますぅ~。
(ちょっと安心して我に返る)
して、あなたの言う、「ことと次第」とは?

アロサウルス

Lukia
んん?
なんておっしゃいました?

ディノ

Lukia

アロサウルス

Lukia
恐竜が数学するなんて、どんなパラレルワールドですかッ!!

アロサウルス

Lukia
アロサウルスさん、高校生なんですかッ?

ディノ

Lukia
ま、とにかく年下ってことですね。
よござんしょ、お教えいたしますッ。
問題
$$\vert x+3 \vert+\vert 2x-4 \vert=8$$

Lukia

ディノ
二つになったもんだから、わかんなくなっちゃったんだよ。

Lukia
じゃ、パターン化してみませんか。

ディノ
こうすれば、解けるってのは、あれば楽でいいよな。

Lukia
じゃ、さっそくやってみましょう。
簡単な図を描こう。

Lukia
こういう図を描いてください。
グラフ自体は、アバウトでオッケーです。
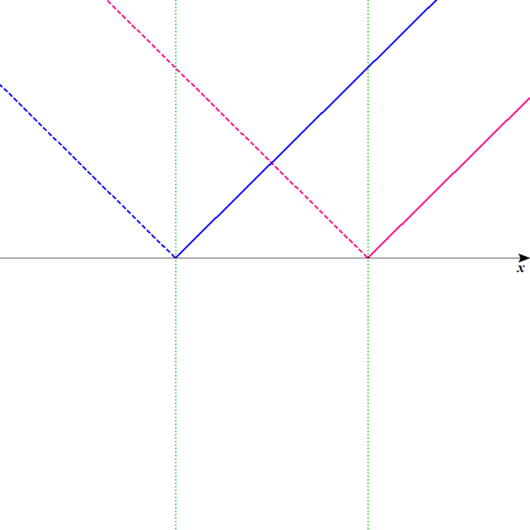

ディノ
\( \ x \ \)軸より下の部分には、グラフがないのに、結構幅が取ってあるな。
なんでだ?

Lukia
最終的には筆算して、答えを求めていくからです。
要するに、計算スペースということになりますね。

ディノ
x軸上にあるのはいつ?

Lukia
ディノさんに出会う前に書いた記事に、
絶対値は、「\( \ x \ \)軸との距離」と読み替えましょう。って書いたんですが、
そのことは、わかってくれますか?

ディノ

Lukia
\( \ x \ \)の値はわかりますか?

ディノ
\(\vert x+3 \vert=0\)
\( \ \pm \left( x+3\right)=0 \ \)ってことだよな。
\( \ x+3=0 \ \) より、\( \ x=-3 \ \)だし、
\( \ -x-3=0 \ \) より、あ、これも\( \ x=-3 \ \)だ。
つまり、\( \ x=-3 \ \)だな。

Lukia
ディノさん、ていねいにやってくれたけど、単純に\( \ x+3=0 \ \)を解いていけばいいことになりますね。
それでは、もう一つの\( \ \vert 2x-4 \vert=0 \ \)はどうですか?

ディノ

Lukia
ということで、先ほどの図に、これらの数字を書き込みます。
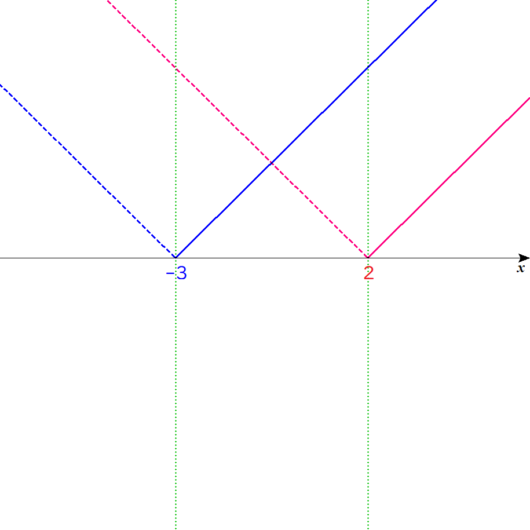

Lukia
試験とか自分で解くときは、鉛筆などでいいですよ。
範囲ごとに、式を書きこんでいく。

Lukia
これによって、三つの範囲に分けられました。
ひとまず、青の線、今回ですと\( \ y=\vert x+3 \vert \ \)にあたりますが、
点線と実線では式が違いますよね。

ディノ
青の実線は、右肩上がりだから、傾きは正ということだから、
\( \ y=x+3 \ \)だな。

Lukia

ディノ
だから、\( \ y=-x-3 \ \)だ。

Lukia
すると、以下のようになりますね。
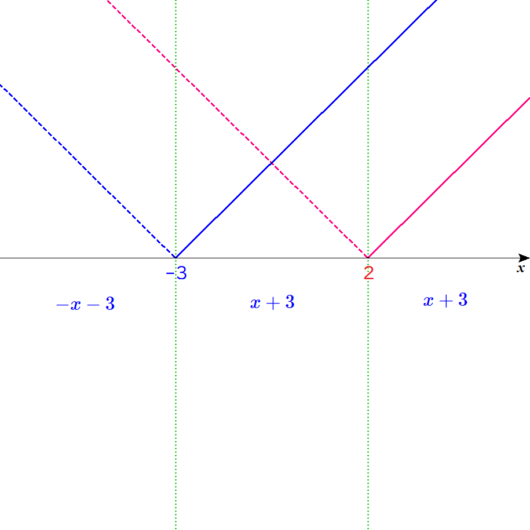

ディノ
ということは、赤い線のグラフも同じようにやればいいのか?

Lukia

ディノ
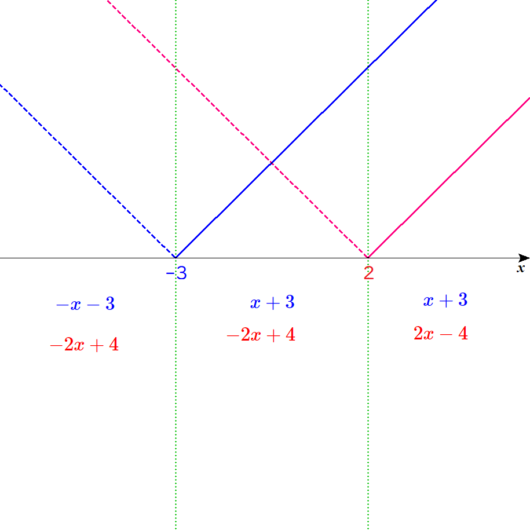
筆算する。

Lukia
それでは、次の段階に進みます。
今回の問題は、絶対値と絶対値が\( \ + \ \)(プラス)でつながれていますね。
ですから、たし算の筆算をします。
ですから、こうなりますね。


Lukia
右辺の\( \ 8 \ \)を\( \ = \ \)(イコール)でつないで、方程式を解いてください。

ディノ

Lukia
範囲と対応しているかどうかは計算した後で考えればよいですから。
方程式を解く。

ディノ
\( \ -3x+1=8 \ \)
\( \ -3x=7 \ \)
\( \ x=-\frac{7}{3} \ \) だ。

ディノ
\( \ -x+7=8 \ \)
\( \ -x=1 \ \)
\( \ x=-1 \ \) だ。

ディノ
\( \ 3x-1=8 \ \)
\( \ 3x=9 \ \)
\( \ x=3 \ \) だ。

Lukia
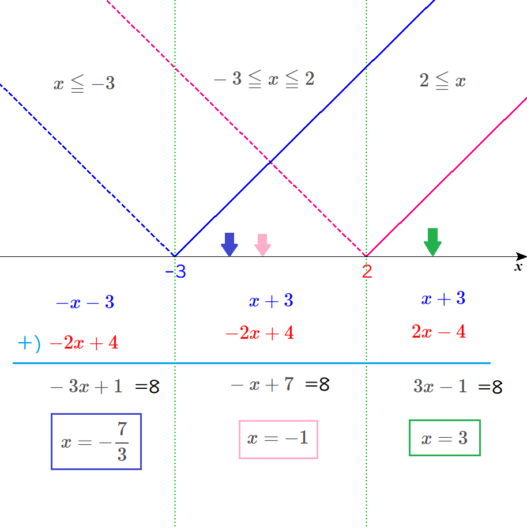
範囲と比較して答えを出す。

Lukia
解のだいたいの位置を矢印で示すとともに、解の値を同じ色の四角で囲んでいます。
方程式の解が、おかしいものはありませんか?


ディノ
・・・
あっ、図の左の解がおかしいな。
解自体は、筆算の結果だから、四角は左の範囲にあるが、
矢印は、真ん中にあるぞ!

Lukia
これは、定義域\( \ x \ \)の値の範囲)からはずれているので、解として正しくない(不適)となります。

ディノ
オマエ、コレ、わかりやすいぞ。

Lukia
こたえ。
$$\Large \vert x+3 \vert+\vert 2x-4 \vert=8$$
$$\Large \begin{align}&x=-1 , x=3 \end{align}$$
ちなみに、グラフはこのようになります。
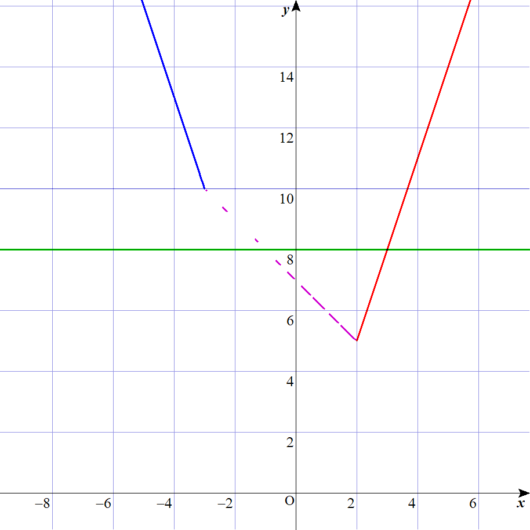

Lukia
青い線は緑の線よりも上にあるため、まったく交わっていませんね。
その後、ディノさんとの会話。

ディノ

Lukia
では、案内をお願いします。

ディノ

Lukia
ディノさん、理解が早いんですから、大丈夫ですよ~。

ディノ
一問教えたぐらいで、偉そうにすんな。

Lukia

ディノ
どうだ、肉食いに行かねぇか?
オレ、いい店知ってるぜ。

有無を言わさずグングン進んでいくディノさんなのでした。
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません