高校数学の絶対値の問題は、グラフでイメージしよう。(その8)

[mathjax]
自宅のパソコンでブログ記事を書いていたはずが、
突然不思議な世界に迷い込み、
高校生?恐竜、ディノさんと出会ってしまった私。
ディノさんは、絶対値の問題の解き方を教えてくれたら、ひらけた場所までの案内をしてくれると言いますが・・・
さて、今回の問題の「解法」で、ディノさんは私を「解放」してくれるのでしょうか。
![]()

Lukia

ディノ

Lukia
私には多すぎるんですよ~。
ディナさんが、せっせと焼いてくれるし。

ディノ
肉を焼くのなんて、なんてこたないんだろ。

Lukia
でも、みなさん、楽しそうでしたね。

ディノ
なんだかんだで、いっつも誰か来てるよなぁ。
つか、オマエもチビたちに人気あったじゃん。

Lukia
あのまま一緒にいたら、もみくちゃにされていたかもしれないので、
ディノさんが、「あっ、そういえば、まだわかんない問題があったんだった!」って言ってくれたのは助かりましたよ。

ディノ

Lukia
問題
$$\Large \color{blue}{\vert x+1 \vert}+\color{red}{\vert x-2 \vert}\leq 5$$
簡単な図を描こう。
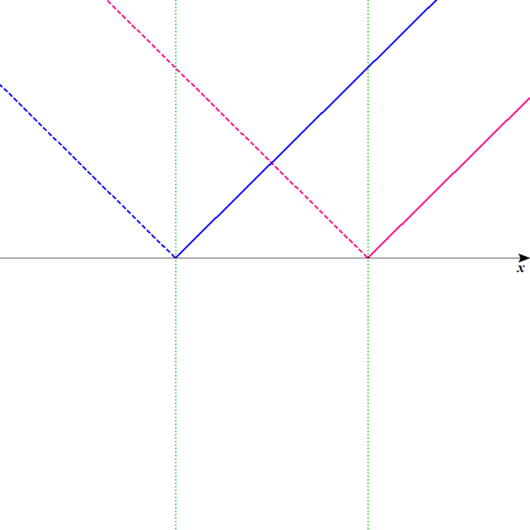

Lukia

ディノ
範囲を設定しよう。

Lukia
範囲を決める段階では、不等式の記号は全く関係ないので、
左辺をやっつけちゃえばいいですね。

ディノ
\( \ \color{blue}{\vert x+1 \vert=0} \ \)となるのは、
\( \ x=\color{blue}{-1} \ \)のときで、
\( \ \color{red}{\vert x-2 \vert=0} \ \)となるのは、
\( \ x=\color{red}{2} \ \)のときだな。

Lukia
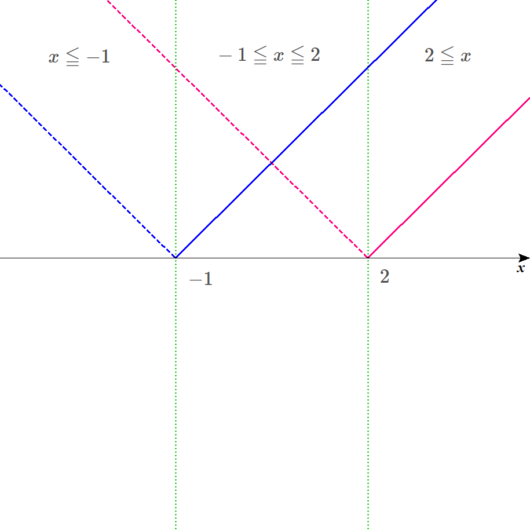
範囲ごとに式を書き込んでいく。

Lukia

ディノ
\( \ \color{blue}{y=\vert x+1 \vert} \ \)は、
\( \ y=\color{blue}{-x-1} \ \) \( \ \left( \color{blue}{x \leq -1} のとき\right ) \ \)
\( \ y=\color{blue}{x+2} \ \) \( \ \left( \color{blue}{-1 \leq x} のとき\right) \ \)となり、

ディノ
\( \ y=\color{red}{-x+2} \ \) \( \ \left( \color{red}{x \leq 2} のとき\right) \ \)
\( \ y=\color{red}{x-2} \ \) \( \ \left( \color{red}{2 \leq x} のとき\right) \ \)となるな。

Lukia
ディノさんは、以下の図のように書き込んでいます。
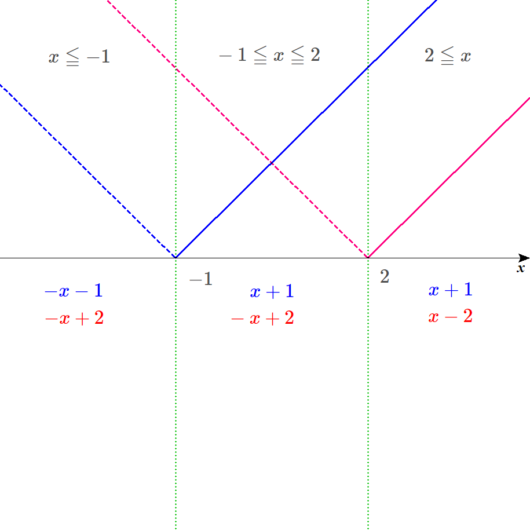
筆算する。

ディノ
今回も、ふたつの絶対値が+(プラス)でつながっているから、
たし算の筆算をすればいいよな。

ディノ
真ん中が、\( \ 3 \ \)
右が \( \ 2x-1 \ \)になるな。
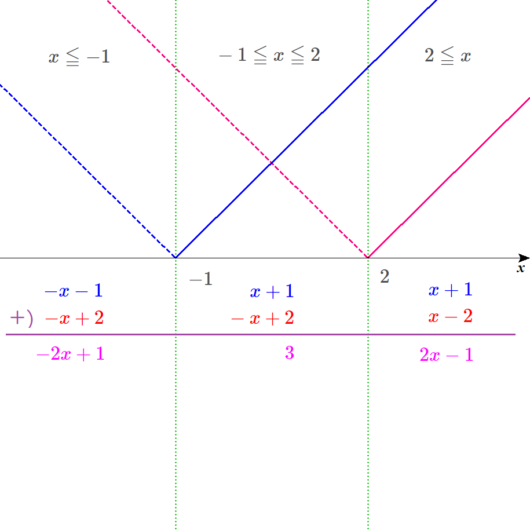
グラフを描くとこうなる。

Lukia


ディノ

Lukia
きれいな台形を保ってるところをみると、結構固めのプリンですね~。
柔らかいプリンもいいけど、スプーンを跳ね返しそうな弾力のあるプリンもおいしいですよねぇ・・・。
そのとき、勉強部屋のドアが、そぉっと閉まりました。
不等式を解く。

Lukia
いよいよ、\( \ \leq 5 \ \) をつけて、不等式を解いてみましょう。

ディノ
左の範囲は、\( \ -2x+1\leq 5 \ \)
\( \ -2 \leq x \ \) だ。

ディノ
まぁ、あたりまえっちゃあたりまえだな。

ディノ
\( \ x \leq 3 \ \)となるな。

Lukia
ちなみに、図は以下のようになりますね。
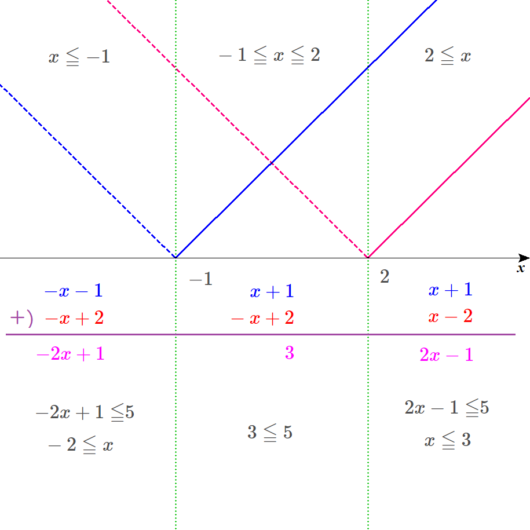
範囲を比較して答えを出す。

Lukia
左の範囲の解は、青い四角で囲み、\( \ x \ \)軸には、青い矢印で、だいたいの位置を示します。
右の範囲の解は、赤い四角で囲み、\( \ x \ \)軸には、赤い矢印で、だいたいの位置を示します。
今回は、わかりやすいように、\( \ x \ \)軸の下に青い線と赤い線で範囲を示しています。
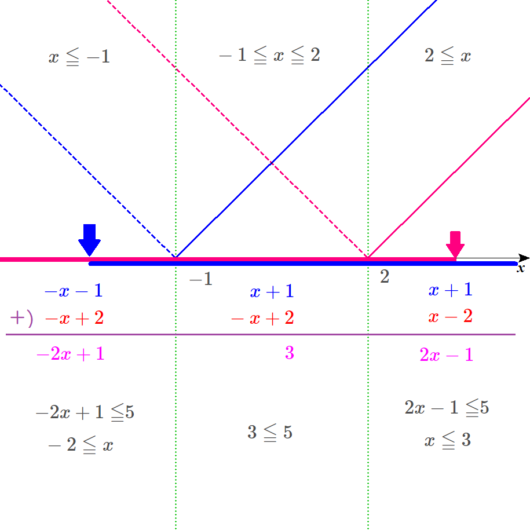

Lukia
真ん中の範囲は、\( \ 3 \leq 5 \ \)と満たしているので、
実は、\( \ -1 \leq x \leq 2 \ \)の範囲で、紫の線が引けることになるんですね。

ディノ
\( \ -2 \leq x \leq 3 \ \)ということか?

Lukia
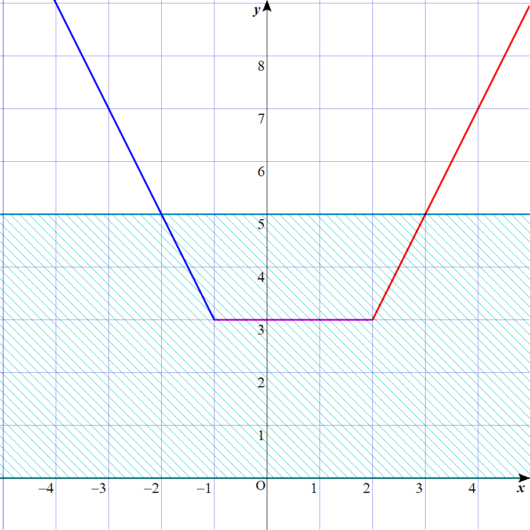
こたえ
$$\Large \vert x+1 \vert+\vert x-2 \vert\leq 5$$
$$\Large -2 \leq x \leq 3$$
ディナさん、再び。

ディナ

ディノ

ディナ
「げっ」とは。(怒)
ディナさんは、恐竜なので、ちょっと怒ってもこわいです。
しかし、私のほうに向きなおると、

ディノ
不出来な息子に教えて、お疲れになったでしょぉ?
おやつにしましょ。おやつ。
甘いもの食べたら、ストレスも疲れもふっとんじゃいますからっ♪

Lukia
それに、朝からいっぱいごちそうになってしまってますし・・・

ディナ
ちなみに、どうザマスか?宅のディノは。

Lukia

ディノ

Lukia

ディノ

ディナ

Lukia
素晴らしいと思います。
もう、私の助けも必要ないかと・・・
それに、お母さん、私は「先生」では・・・。

ディノ
宅のディノをそんなに褒めていただいてッ。
ディノ~、いい先生が見つかってよかったわねぇ~。
さっ、センッセ、おやつにいたしましょッ。
先ほど、プリンのお話が出てましたでしょ?
作りましたのよッ♪

ディノ
かーちゃんのは、うめぇんだぞ!
ディノさんまで、テンションが上がってしまい、私は、帰りたいと言い出せなくなってしまいました。
ダイニングに行くと、先ほど一緒にバーベキューをした近所のお母さん恐竜や、チビ恐竜たちが、
嬉しそうにプリンを食べていました。
みんな、ディナさんの姉御肌気質が大好きで、居心地がいいのか、
楽しそうにおしゃべりをしています。
なんだか、それを見ていると、帰ることばかり考えていた私の気持ちも少し変わってきました。
ディノさんは、一応「ひらけた場所」に案内してくれるつもりではいるようですから、
ディノさんの問題が解決するまでは、お世話になろうと思いました。
そして、出てきたプリンのおいしいこと!


Lukia

ディナ
たくさんあるから、遠慮なく召し上がってねッ。
恐竜サイズですから、ひとつで十分です・・・
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません