Yahoo!知恵袋で見つけた高校数学の「回転体の体積」を求めてみる。

[mathjax]
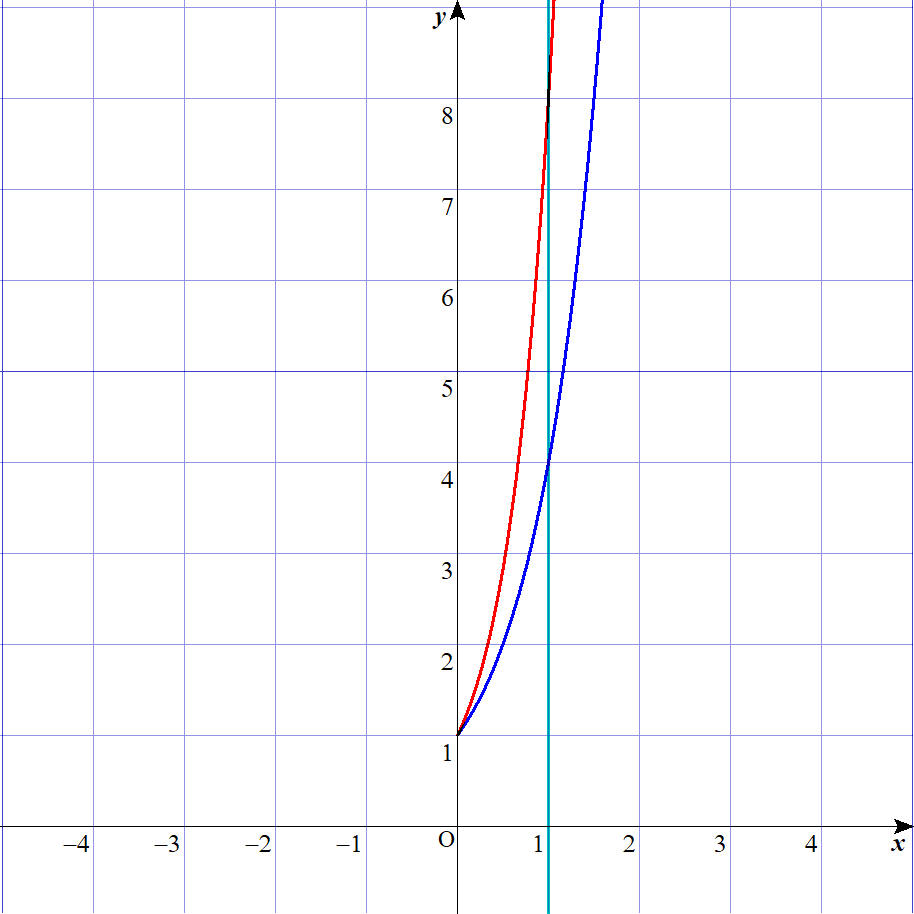
まず、こんな図。

Lukia
\(y=8^x\)を赤い曲線で示し、
\(x=1\)を緑の直線で示します。
$$x軸回転$$
まずは、V1

Lukia
すると、盃のような形ができます。
盃は、中がくぼんでいるので、飲み物を入れることができますが、\(x=1\)という、直線でスパン!と切られているので、盃というよりは、お皿というほうがいいかもしれませんね。

Lukia
この赤い曲線と\(x=1\)によってできる回転体の体積を、\(\color{red}{V_1}\)とします。
$$\Large \color{red}{V_1}=\pi\int_{0}^{1} \left( 4^x\right)^2 dx$$

次にV2

Lukia
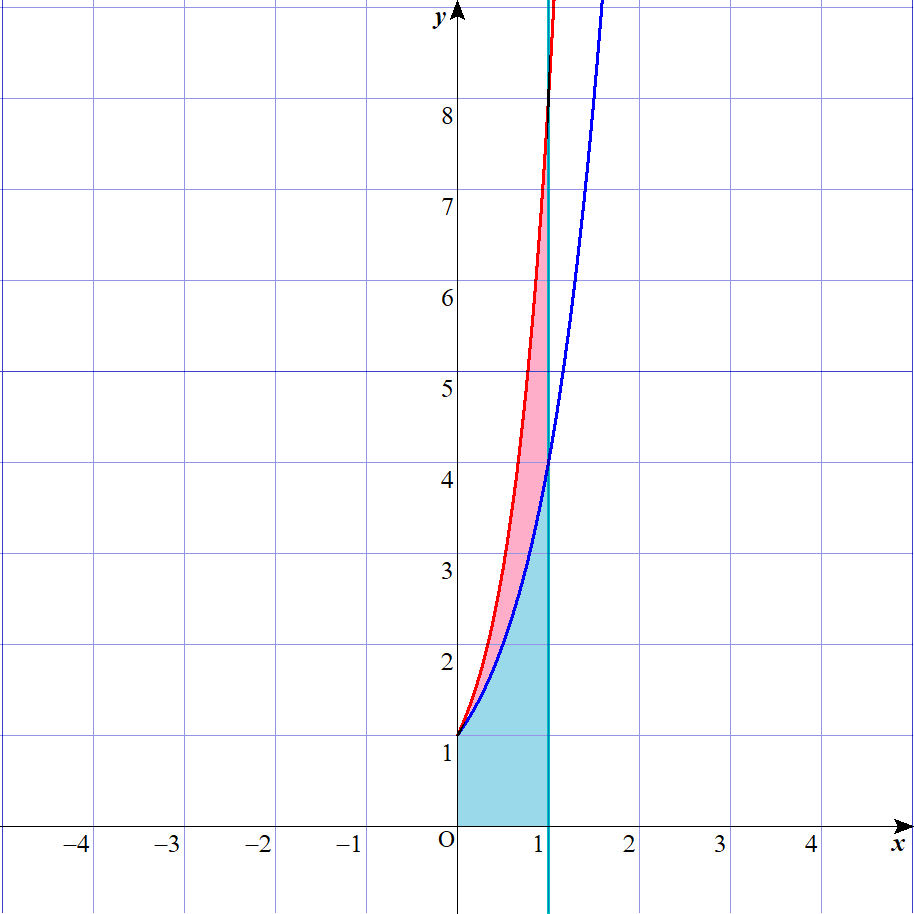
すると、下の図のように、水色で塗りつぶされている範囲ができます。
今回求めるのは、赤と青の曲線と、緑の直線で囲まれた部分ですから、ピンクで塗りつぶした部分を回転させることになります。
(水色の部分は、いらないので、削り取ります。)
これまでは、お皿のような状態でしたが、水色の部分が削り取られることで、じょうごのような形になります。
バウムクーヘンでもいいですが、食べるところは極端に少なくなりそうですね。(笑)

Lukia
$$\Large \color{blue}{V_2}=\pi\int_{0}^{1} \left( 4^x\right)^2 dx$$
いよいよVを求める。

Lukia
\(\Large V=\color{red}{V_1}-\color{blue}{V_2}\)
によって求められるので、
$$\begin{align}V&=\color{red}{V_1}-\color{blue}{V_2} \\\\ &=\pi\int_{0}^{1}\left( \left( 8^x\right)^2-\left( 4^x\right)^2\right) dx \\\\ &=\pi\int_{0}^{1}\left( 2^\left( 6x\right)-2^\left( 4x\right)\right) dx \\\\ &=\pi\int_{0}^{1}\left( \left( 2^x\right)^6-\left( 2^x\right)^4\right) dx \end{align}$$

Lukia
\(x=\log_{2}t=\frac{1}{\log 2}\log t\)
これを\(x\)について微分します。
$$\begin{align}x&=\frac{1}{\log 2}\log t をxについて微分する。 \\\\ 1&=\frac{1}{\log 2}\cdot \frac{1}{t}\frac{ \mathrm{ d } t }{ \mathrm{ d } x } \\\\整理して、 dx&=\frac{1}{\log 2}\cdot \frac{1}{t}dt \end{align}$$

Lukia
$$\begin{align}V&=\pi\int_{1}^{2} \left( t^6-t^4\right)\cdot \frac{1}{\log 2}\cdot \frac{1}{t} dt \\\\ &=\frac{\pi}{\log 2}\int_{1}^{2} \left( t^6-t^4\right)\cdot \frac{1}{t} dt \\\\ &=\frac{\pi}{\log 2}\int_{1}^{2} \left( t^5-t^3\right)dt\\\\ &=\frac{\pi}{\log 2}\left[\frac{1}{6}t^6-\frac{1}{4}t^4\right]_{1}^{2}\\\\ &=\frac{\pi}{\log 2}\lbrace \frac{1}{6}\left(64-1 \right)-\frac{1}{4}\left( 16-1\right)\rbrace \\\\ &=\frac{\pi}{\log 2}\left( \frac{21}{2}-\frac{15}{4}\right)\\\\ &=\frac{\pi}{\log 2}\cdot \frac{27}{4}\\\\ &=\frac{27\pi}{4\log 2} \end{align}$$

Lukia
$$y軸回転$$
式や定義域・値域をとらえなおす。

Lukia
これを\(x=f\left( y\right)\) という形に直していきます。定義域や値域も入れ替わりますね。

Lukia
定義域が\(\Large \color{red}{\left( 0 \leq x \leq 1\right)}\)であり、
値域は、\(\Large \color{red}{\left( 1 \leq y \leq 8\right)}\)でしたが、

Lukia
定義域が\(\Large \color{red}{\left( 1 \leq y \leq 8\right)}\)
値域は、\(\Large \color{red}{\left( 0 \leq x \leq 1\right)}\)となります。

Lukia
定義域が\(\Large \color{blue}{\left( 0 \leq x \leq 1\right)}\)であり、
値域は、\(\Large \color{blue}{\left( 1 \leq y \leq 4\right)}\)でしたが、

Lukia
定義域が\(\Large \color{blue}{\left( 1 \leq y \leq 4\right)}\)
値域は、\(\Large \color{blue}{\left( 0 \leq x \leq 1\right)}\)となります。
図からすると・・・
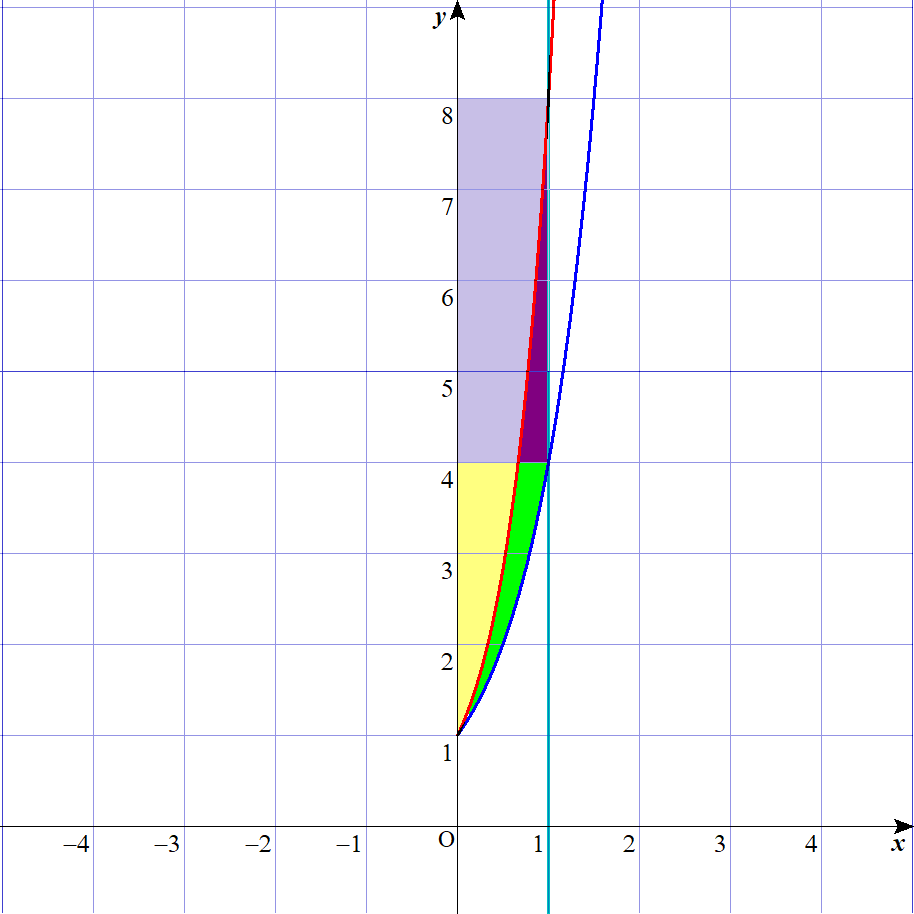

Lukia
\(x\)軸回転のときは、赤い曲線も、青い曲線も定義域が\(\left( 0 \leq x \leq 1\right)\)であったため、インテグラルも一つでよかったのですが、
今回は、定義域が異なっていますね。
また、\(\left( 1 \leq y \leq 4\right)\) までは、赤い曲線と青い曲線によって、緑の部分が囲まれていますが、
\(\left( 4 \leq y \leq 8\right)\) に関しては、赤い曲線と緑直線によって、濃い紫の部分が囲まれています。
というわけで、二段階に分けて、回転体の体積を求めていきます。
式を立てる。
$$\begin{align}&求める回転体の体積をVとする。\\\\ \frac{V}{\pi}&= \int_{1}^{4} \left( \left( log_{4}y\right)^2-\left( \log_{8}y\right)^2\right) dy+\int_{4}^{8} \left( 1^2-\left( \log_{8}y\right)^2\right) dy\\\\ &=\frac{5}{36}\int_{1}^{4} \left( \frac{\log y}{\log 2}\right)^2 dy +\int_{4}^{8} 1-\frac{1}{9}\left( \frac{\log y}{\log 2}\right)^2 dy \\\\ &=\frac{5}{36\left( \log 2\right)^2} \int_{1}^{4} \left( \log y\right)^2 dy+\int_{4}^{8} 1 dy-\frac{1}{9\left( \log y\right)^2}\int_{4}^{8} \left( \log y\right)^2 dy\end{align}$$

Lukia
両辺を\(y\)について微分すると、
\(\Large \frac{1}{y}=\frac{ \mathrm{ d } t }{ \mathrm{ d } y }\) より、
\(\Large dy=y dt\)
また、\(\Large y=e^t\)より、
\(\Large dy=e^t dt\) である。
$$\begin{align}与式&=\frac{5}{36\left( \log 2\right)^2} \int_{0}^{\log 4} t^2\cdot e^t dt+4-\frac{1}{9\left( \log 2\right)^2}\int_{\log 4}^{\log 8} t^2\cdot e^t dt\end{align}$$

Lukia
$$\begin{align}与式&=\color{red}{\frac{5}{36\left( \log 2\right)^2}\lbrace F\left( \log 4\right)-F\left( 0\right)\rbrace} +4-\color{blue}{\frac{4}{36\left( \log 2\right)^2}\lbrace F\left( \log 8\right)-F\left( \log 4\right)\rbrace}\\\\ &=\color{magenta}{\frac{9}{36\left( \log 2\right)^2}F\left( \log 4\right)} +4\color{red}{-\frac{5}{36\left( \log 2\right)^2}F\left( 0\right)}\color{blue}{-\frac{4}{36\left( \log 2\right)^2}F\left( \log 8\right)} \\\\ &=\color{magenta}{\frac{9}{36\left( \log 2\right)^2}F\left( 2\log 2\right)} +4\color{red}{-\frac{5}{36\left( \log 2\right)^2}F\left( 0\right)}\color{blue}{-\frac{4}{36\left( \log 2\right)^2}F\left( 3\log 2\right)} \end{align}$$

Lukia
\(\Large F\left( t\right)=\int t^2\cdot e^t dt=e^t\left( t^2-2t+2\right)+C\)
(\(C\)は積分定数) だから、
$$\begin{align}与式&=\color{magenta}{\frac{9}{36\left( \log 2\right)^2}e^\left( \log 4\right)\lbrace \left( 2\log 2\right)^2-4\log 2+2\rbrace} +4\\\\ & \color{red}{-\frac{5}{36\left( \log 2\right)^2}e^0\cdot 2}\color{blue}{-\frac{4}{36\left( \log 2\right)^2}e^\left( \log 8\right)\lbrace \left( 3\log 2\right)^2-6\log 2+2\rbrace} \end{align}$$

Lukia
\(\Large e^\left( \log \alpha\right)=\alpha\) より
$$\begin{align}与式&=\color{magenta}{\frac{1}{\left( \log 2\right)^2}\lbrace 4\left( \log 2\right)^2-4\log 2+2\rbrace}+4\\\\ & \color{red}{-\frac{10}{36\left( \log 2\right)^2}} \color{blue}{-\frac{32}{36\left( \log 2\right)^2}\lbrace 9\left( \log 2\right)^2-6\log 2+2\rbrace}\\\\ &=\color{magenta}{4-\frac{4}{\log 2}+\frac{2}{\left( \log 2\right)^2}}+4\\\\ & \color{red}{-\frac{5}{18\left( \log 2\right)^2}} \color{blue}{-8+\frac{16}{3\log 2}-\frac{16}{9\left( \log 2\right)^2}}\\\\ &=\frac{1}{\log 2}\left( -4+\frac{16}{3}\right) +\frac{1}{\left( \log 2\right)^2}\left( 2-\frac{5}{18}-\frac{16}{9}\right)\\\\ &=\frac{1}{\log 2} \cdot \frac{4}{3}+\frac{1}{\left( \log 2\right)^2}\cdot \left( -\frac{1}{18}\right) \\\\ &=\frac{24\log 2-1}{\left( \log 2\right)^2} \end{align}$$
$$\Large ゆえに、V=\frac{\left( 24\log 2-1\right)\pi}{\left( \log 2\right)^2}$$

Lukia
値そのものには、ちょっと自信がありません。
(うっかりミスをやらかすもので・・・)
Dという形は同じなのに・・・

Lukia
回転させるのが、\(x\)軸なのか、\(y\)軸なのかで、まったく値が変わってしまうんですね。
もし、これが入試問題として出たら、相当大変だろうと思います。
スピーディで、正確な計算力と、長い計算を途中で不安にならず、しっかり集中力を保った状態でこなせる精神力が必要ですね。
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません