高校数学の「2次方程式の実数解」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月12日2023年1月14日数と式実用数学技能検定（数学検定数検),数検準2級

読了時間: 約3分51秒

[mathjax]

問題

$x$についての2次方程式 $ \ x^2-2\left( k+2\right)x+k^2+2k+3=0 \ $ $ \ \left( k \ は実数\right) \ $が異なる二つの実数解をもつとき,$ \ k \ $のとり得る値の範囲は,$ \ k \gt \frac{\color{red}{[アイ]}}{\color{red}{[ウ]}} \ $であり,二つの実数解は,
$x=k+\color{red}{[エ]} \pm \sqrt{\color{red}{[オ]}k+\color{red}{[カ]}}$である.
二つの実数解を$ \ \alpha, \ \beta \ \left( \alpha \lt \beta\right) \ $とするとき,$ \ \alpha+\beta=\color{red}{[キ]}k+\color{red}{[ク]} \ $である.
$ \ \frac{\alpha+\beta}{3} \ $の値の小数第1位を四捨五入すると$ \ 6 \ $になるとき,$ \ k \ $のとり得る値の範囲は,
$\frac{\color{red}{[ケコ]}}{\color{red}{[サ]}} \leq k \lt \frac{\color{red}{[シス]}}{\color{red}{[セ]}}$である.
次に,$ \ k \ $を整数とする.不等式$ \ \alpha \lt x \lt \beta \ $を満たす整数$ \ x \ $が3個だけ存在するような整数$ \ k \ $の値は$\color{red}{[ソ]}$である.

ア～クまでは確実にできるようであってほしい。

与式の判別式をDとするとき,
$$\begin{align}\mathrm{D}/4=\left( k+2\right)^2-\left( k^2+2k+3\right) \gt &0 \\ 2k+1 \gt &0 \\ k \gt &-\frac{1}{2} \end{align}$$
与式の二つの異なる実数解は
$$\begin{align}x=&k+2 \pm \sqrt{2k+1} \end{align}$$
二つの実数解の和は
$$\alpha+\beta=2k+4$$

ケ～セを解く。

$$\begin{align}\alpha+\beta=&2k+4 \gt 2\cdot \left( -\frac{1}{2}\right)+4 \\ \frac{\alpha+\beta}{3}=&\frac{2k+4}{3} \gt 1\end{align}$$

Lukia

この操作で、$ \ \frac{\alpha+\beta}{3} \ $が明らかに1より大きいとわかりますね。

$$四捨五入して \ 6 \ になる \ \frac{\alpha+\beta}{3} \ は,$$
$$\begin{align}5.5 \leq &\frac{\alpha+\beta}{3} \lt 6.5 \\ \frac{3\times 55}{10} \leq &2k+4 \lt \frac{3\times 65}{10} \\ \frac{3\times 55-40}{10} \leq &2k \lt \frac{3\times 65-40}{10}\\ \frac{25}{4} \leq &k \lt \frac{31}{4} \end{align}$$

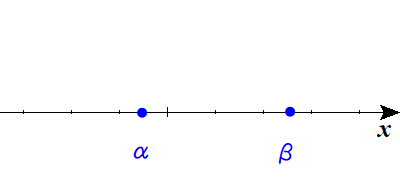
ソを高精度で解くポイントは平方根。

二つの実数解の差が3以上で4より小さければよい。
$$\begin{align}\beta-\alpha=&2\sqrt{2k+1} \\ 3 \leq &2\sqrt{2k+1} \lt 4 \\ 3 \leq &\sqrt{8k+4} \lt 4 \end{align}$$

Lukia

$ \ 2\sqrt{2k+1} \ $を$ \ \sqrt{8k+4} \ $にすることで、答えの精度が上がります。

$$\begin{align}3 \leq &\sqrt{8k+4} \lt 4\\ \sqrt{9} \leq &\sqrt{8k+4} \lt \sqrt{16}\end{align}$$
以下は平方根をはずして考える.
$$\begin{align}9 \leq &8k+4 \lt 16 \\ 5 \leq &8k \lt 12 \\ \frac{5}{8} \leq &k \lt \frac{3}{2} \end{align}$$

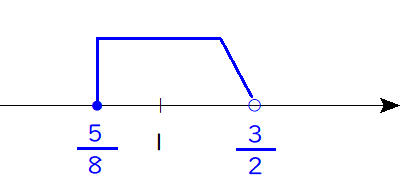
$$題意を満たす整数 \ k \ は \ 1 \ $$

こたえ

$$\frac{\color{red}{[アイ]}}{\color{red}{[ウ]}}$$	$$\frac{\color{red}{-1}}{\color{red}{2}}$$
$$k+\color{red}{[エ]} \pm \sqrt{\color{red}{[オ]}k+\color{red}{[カ]}}$$	$$k+\color{red}{2} \pm \sqrt{\color{red}{2}k+\color{red}{1}}$$
$$\color{red}{[キ]}k+\color{red}{[ク]}$$	$$\color{red}{2}k+\color{red}{4}$$
$$\frac{\color{red}{[ケコ]}}{\color{red}{[サ]}}$$	$$\frac{\color{red}{25}}{\color{red}{4}}$$
$$\frac{\color{red}{[シス]}}{\color{red}{[セ]}}$$	$$\frac{\color{red}{31}}{\color{red}{4}}$$
$$\color{red}{[ソ]}$$	$$\color{red}{1}$$

関連

プロフィール

Author Profile

Lukia_74

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。

カテゴリー