高校数学の「連立二次不等式」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約1分21秒
[mathjax]
問題
\(x\)についての二つの二次不等式
\(2x^2-3x-9 \gt 0 \cdots ①\)
\(x^2-2ax+a^2-1 \lt 0 \cdots ②\)
を同時に満たす整数\(x\)が存在しないように、
定数\(a\)の値の範囲を求めよ。
\(2x^2-3x-9 \gt 0 \cdots ①\)
\(x^2-2ax+a^2-1 \lt 0 \cdots ②\)
を同時に満たす整数\(x\)が存在しないように、
定数\(a\)の値の範囲を求めよ。
二つの二次不等式を解いてみる。
$$\begin{align}①を解く。&\\\\ 2x^2-3x-9 \gt &0 \\\\ \left( x-3\right)\left( 2x+3\right) \gt &0\\\\ x \lt -\frac{3}{2} , 3 \lt x \cdots ①\end{align}$$
$$\begin{align}②を解く。& \\\\ x^2-2ax+a^2-1 \lt &0 \\\\ \left( x-a\right)^2-1^\color{red}{2} \lt &0\\\\ \left( x-a+1\right)\left( x-a-1\right) \lt 0\\\\ a-1 \lt x \lt a+1 \cdots ②\end{align}$$
定数aの範囲を定めていく。
Lukia
以下の画像は、①の不等式が示す\(x\)の値の範囲を青い線で示しています。
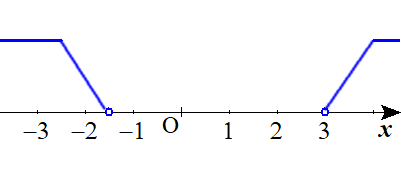
Lukia
この数直線を見ると、左の範囲には\(-2\)以下の整数が存在し、
右の範囲には\(4\)以上の整数が含まれています。
右の範囲には\(4\)以上の整数が含まれています。
Lukia
ということは、②の不等式が示す\(x\)の値の範囲が、左端は\(-2\)よりも大きく、
右端が\(4\)よりも小さければよいことになります。
右端が\(4\)よりも小さければよいことになります。
$$\begin{align}条件を満たすには &定数aが \\\\ -2 \lt &a-1 \ かつ \ a+1 \lt 4 \ を満たせばよい. \\\\ゆえに\quad &-1 \lt a \lt 3 \end{align}$$
こたえ
$$-1 \lt a \lt 3$$
共有:
プロフィール
Author Profile
