高校数学の「等差数列にひそむ飛び石のような数列」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
また数列\(\lbrace b_n\rbrace\)は\(b_1=a_3, \ b_2=a_9, \ b_3=a_{27} \ \cdots \ b_n=a_{3^n}\)を満たしているとする。
数列\(\lbrace a_n\rbrace\)のうち、数列\(\lbrace b_n\rbrace\)の項を除いて、小さいものから順に並べた数列を\(\lbrace c_n\rbrace\)とする。数列\(\lbrace c_n\rbrace\)の初項から第100項までの和を求めよ。
まずは等差数列{a_n}を明らかにする。
$$\begin{align}等差数列\lbrace a_n\rbrace & \ の初項を \ a, \ 公差をd \ とする。\\\\ a_1+a_2+a_3=&a+a+d+a+2d \\\\ =&3a+3d=21 \ より\\\\ a+d=&7 \\\\ さらに \ a_5=a+4d=&16 \ との連立方程式を解いて,\\\\ &a=4,\quad d=3 \end{align}$$
$$ゆえに \ 等差数列\lbrace a_n\rbrace \ は,\quad a_n=3n+1\quad である.$$
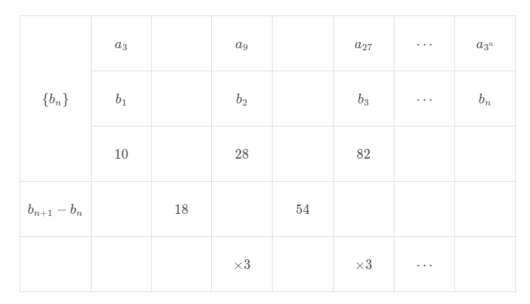
数列{b_n}を明らかにする。

Lukia

Lukia
$$\begin{align}b_n=&b_1+\sum_{k=1}^{n-1}{18\cdot 3^{k-1}} \\\\ =&10+\frac{18-18\cdot 3^{n-1+1}}{1-3} \\\\ =&3^{n+1}+1\\\\ これは&n=1 \ のときも成り立つ. \end{align}$$
数列{a_n}と数列{b_n}の関係性を解明する。

Lukia
$$\begin{align}数列\lbrace c_n\rbrace \ の項数は&3^n-n\quad で求められる. \\\\ 3^n-n \leq &100 \\\\ 3^n \leq &100+n \end{align}$$
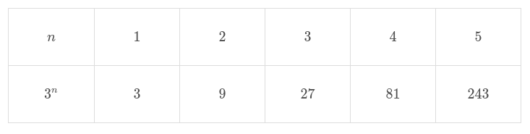
$$上の表より、n=4 \ のとき条件を満たすことがわかる.$$
$$\begin{align}\sum_{k=1}^{100}{c_k}=&\sum_{k=1}^{104}{a_k}-\sum_{k=1}^{4}{b_k} \\\\ =&\frac{104}{2}\left( 4+3\times 104+1\right)-\left( \frac{9-3^{5+1}}{1-3}+4\right) \\\\ =&52\times 317+\frac{3^2}{2}\left( 1-3^4\right)-4\\\\ =&16484-40\times 9-4 \\\\ =&16120 \end{align}$$
こたえ
$$16120$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません