高校数学の「2つの二次方程式が成り立つ範囲」に関する問題を解いてみる。(Yahoo!知恵袋より)

読了時間: 約1分35秒
[mathjax]
問題
次の2つの2次方程式がどちらも異なる2つの解を持つような\(m\)の範囲を求めよ。
\(x^2+2mx+m^2-2m+4=0・・・①\)
\(x^2-4x+m\left( m-3\right)=0・・・②\)
\(x^2+2mx+m^2-2m+4=0・・・①\)
\(x^2-4x+m\left( m-3\right)=0・・・②\)
2次方程式から二次関数にイメージ化する。

Lukia
①と②の式を\(x\)に関する二次関数(放物線)ととらえたとき、
どちらのグラフも、\(x\)軸と2ヵ所で交わりなさい。と言われていることになります。
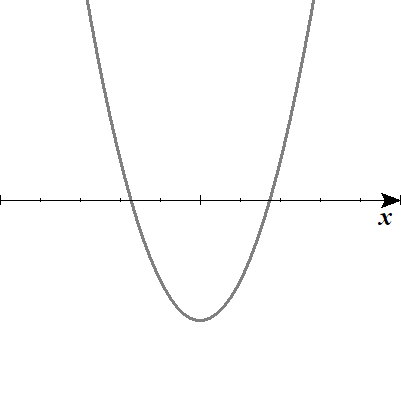
簡単な図を描くと、以下のようになりますね。
どちらのグラフも、\(x\)軸と2ヵ所で交わりなさい。と言われていることになります。
簡単な図を描くと、以下のようになりますね。

Lukia
どちらも、「下に凸」の関数ですから、
①と②が条件を満たすには、
頂点の\(y\)座標が負である必要があります。
①と②が条件を満たすには、
頂点の\(y\)座標が負である必要があります。
頂点を求める。
$$\begin{align}①をf\left( x\right)=&x^2+2mx+m^2-2m+4 \\\\ ②をg\left( x\right)=&x^2-4x+m\left( m-3\right) としたとき\\\\ 条件を満たすには,&f\left( x\right)とg\left( x\right) \\\\ の頂点のy座標が負であればよい. \end{align}$$
$$\begin{align}y=&f\left( x\right) \ の頂点を求める。 \\\\ 与式=&\left( x+m\right)^2-2m+4\quad より \\\\ 頂点は&\left( -m \ , \ -2m+4\right) \end{align}$$
$$\begin{align}y=&g\left( x\right) \ の頂点を求める。 \\\\ 与式=&\left( x-2\right)^2-4+m^2-3m\quad より \\\\ 頂点は&\left( 2 \ , \ m^2-3m-4\right) \end{align}$$
ゆえに、
$$\begin{align}-2m+4 \lt 0\quad かつ\quad m^2-3m-4 \lt 0\quad を満たす\ mの範囲を求める。\end{align}$$
$$\begin{align}2 \lt m\quad かつ \ -1 \lt m \lt 4\ \\\\ ゆえに求めるmの範囲は\quad 2 \lt m \lt 4\end{align}$$
こたえ
$$2 \lt m \lt 4$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません