高校数学の「絶対値が絡んだ積分」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年10月24日2023年1月15日微分と積分実用数学技能検定（数学検定数検),数検2級

読了時間: 約5分6秒

問題

$1 \lt x$の範囲で$x$が変化するとき、
$f\left( x\right)=\int_{1}^{2} \vert t^2-xt \vert dt$を最小にする$x$の値を求めよ。
出典：文系の数学重要事項完全習得編 (河合塾シリーズ)

文系の数学（重要事項完全習得編）（河合塾series） [ 堀尾豊孝 ]

楽天で購入

絶対値をはずそう。

ディノ

あっ、またこないだと同じ記号だな！
そして、絶対値の記号もあるぞ！

Lukia

この記事でやりましたね。

高校数学の「積分とその応用・絶対値を含む積分」に関する問題を解いてみる。（Yahoo!

問題 $\int_{0}^{2} \vert e^x-3 \vert dx$ を求めよ。絶対値が含まれてるぞ！ディノうおぉ、なん ...

https://makelemonadejp.com/yc-31

Lukia

では、ディノさん、
$g\left( t\right)=\vert t^2-xt \vert$　として、絶対値をはずしてもらえますか。

ディノ

いいぞ。もうこれは簡単・・・
ていうか、$x$をどう扱ったらいいんだ？

Lukia

これは、$t$に関する式なので、
$x$は、定数扱いなんですよ。1とか$a$みたいなね。

ディノ

じゃ、数みたいに扱っていいってことだな。
それなら、簡単だ。

$$\begin{align}g\left( t\right)=&\vert t^2-xt \vert \\\\ 1 \lt x&より、 \\\\ g\left( t\right)=&t^2-xt\quad \left(t \leq 0 \ , \ x \leq t\right)
\\\\ g\left( t\right)=&-\left( t^2-xt\right)\quad \left( 0 \lt t \lt x\right) \end{align}$$

Lukia

「$1 \lt x$より、」なんて入れたところがニクいですね。
「オレは、$x$と$0$との大小関係、ちゃ～んとわかってるぜ。」っていうアピールになりますね。
ちなみに、だいたいでいいので、グラフも描けますか？

ディノ

おう。こうだな。

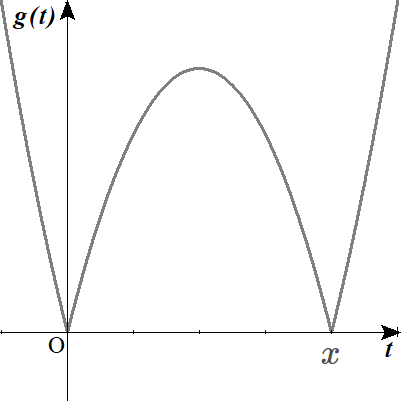
2とxの大小関係に注意して、式を立てる。

Lukia

さて、積分区間が$1$から$2$となっているわけですが、
$1 \lt x$という条件より、
$1$は、グラフの上に凸の区間に含まれていることは間違いないですね。

ディノ

そうだな。

Lukia

では、$2$はどうでしょう。

ディノ

$1$と$x$との大小関係ははっきりしているが、
$2$と$x$の大小関係はわかんねぇな。

Lukia

つまり？

ディノ

$ 2\leq x$だったら、$2$は、上に凸のところに含まれるし、
$x \lt 2$だったら、グラフだと下に凸の曲線の右側に含まれるよな。

Lukia

下の図では、$1$のだいたいの位置を決めています。
今回も問題では、$1$の位置より、$2$の位置が重要なので、このぐらいアバウトでかまいません。
そして、$2$の位置は、①と②とありますが、それぞれわかりますか？

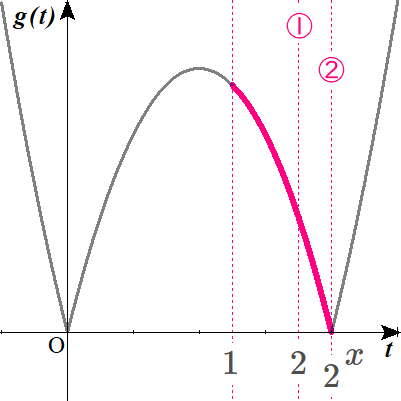
ディノ

①は、$2 \lt x$ のときだ。
明らかに小さいときだな。

ディノ

そして、②は、$x=2$のときだ。
ぴったり重なっているときだな。

Lukia

そうです。
では、$x \lt 2$のときも考えてみましょう。
以下の図のようになりますね。

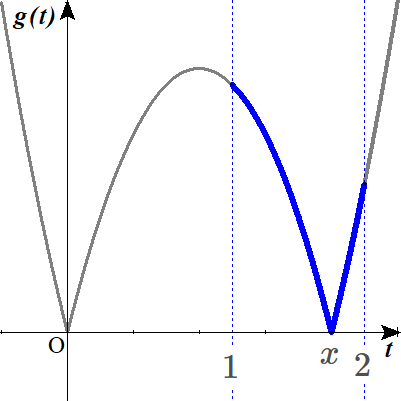
Lukia

この図を参考に式を立てていきます。

ⅰ）を解く。

$$\begin{align}ⅰ） \color{#f700ca}{t軸において、}\ & 2 \leq x \ のとき、 \\\\ f\left( x\right)=&-\int_{1}^{2} \left( t^2-xt\right) dt \\\\ =&-\left[\frac{1}{3}t^3-\frac{1}{2}xt^2\right]_{1}^{2}\\\\ =&-\lbrace \frac{1}{3}\left( 8-1\right)-\frac{1}{2}x\left( 4-1\right)\rbrace\\\\ =&-\frac{3}{2}x-\frac{7}{3}\quad \left( 2 \leq x\right) \end{align}$$

Lukia

ⅰ）のグラフは、右下がりの直線ですから、最小値は定められません。
ゆえに不適となります。

ⅱ）を解く。

$$\begin{align}ⅱ）\quad \color{#f700ca}{t軸において} \\\\ &1 \lt x \lt 2 \ のとき \\\\ f\left( x\right)=&-\int_{1}^{x} \left( t^2-xt\right) dt+\int_{x}^{2} \left( t^2-xt\right) dt \end{align}$$
$$\begin{align}ここで、 \\\\ g\left( t\right)&の原関数を \\\\ \mathrm{G}\left( t\right) \ とする。 \\\\ \mathrm{G}\left( t\right)=&\frac{1}{3}t^3-\frac{1}{2}xt^2 \end{align}$$
$$\begin{align}f\left( x\right)=&-\mathrm{G}\left( x\right)+\mathrm{G}\left( 1\right)+\mathrm{G}\left( 2\right)-\mathrm{G}\left( x\right) \\\\ =&\mathrm{G}\left( 2\right)+\mathrm{G}\left( 1\right)-2\mathrm{G}\left( x\right) \\\\ =&\frac{1}{3}x^3-\frac{5}{2}x+3\quad \left( 1 \lt x \lt 2\right) \end{align}$$

Lukia

$f\left( x\right)$の概形を知るため、微分して増減表をかきます。

$$\begin{align}f’\left( x\right)=&x^2-\frac{5}{2} \\\\ f’\left( x\right)=&0 \ となるのは \\\\ x=& \pm \frac{\sqrt{10}}{2} \end{align}$$

ここで、
$$\frac{3}{2} \lt \frac{\sqrt{10}}{2} \lt 2$$

増減表は以下の通り。

$$x$$	・・・	$$-\frac{\sqrt{10}}{2}$$	・・・	$$1$$	$$\frac{\sqrt{10}}{2}$$	$$2$$	・・・
$$f’\left( x\right)$$	$$+$$	$$0$$	$$-$$		$$0$$	$$+$$
$$f\left( x\right)$$	↗	（極大値）	↘		（極小値）最小値	↗