Yahoo!知恵袋の高校数学カテゴリにあった「最大値・最小値」問題を解いてみる。

2018年9月23日2023年1月15日微分とその応用実用数学技能検定（数学検定 数検),数検準1級

[mathjax]

解法

Lukia

最大値・最小値という言葉を見たら、
微分して、できるだけ正確なグラフをとらえる必要があります。
また、以下のような図を描いて、スピーディに微分していきましょう。

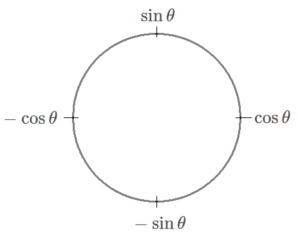
$$\begin{align}y=&f(x)　とする。
\\\\ f'(x)=&\color{blue}{-\sin x}\cdot \sin x+\left( 1+\cos \theta\right)\color{blue}{\cos x}
\\\\ =&-\sin^{2} x+\cos^{2} x+\cos^{2} x
\\\\ =&2\cos^{2} x+\cos x-1 \end{align}$$

$$\begin{align}ここで、f’\left( x\right)=0　になるときを考える。
\\\\ \left( \cos x+1\right)\left( 2\cos x-1\right)=&0
\\\\ \cos x=-1 ,　\cos x=\frac{1}{2}
\\\\ 範囲より、x=\pi　,　\frac{ \pi }{ 3 }　,　{\frac{ 5 }{ 3 }}\pi \end{align}$$
これをもとに、増減表を書いてみる。

$$\begin{align}ゆえに、&
\\\\ 最大値：&　 \frac{3\sqrt{3}}{4}
\\\\ 最小値：&　 -\frac{3\sqrt{3}}{4}\end{align}$$

こたえ

$$\begin{align} 最大値：　 &\frac{3\sqrt{3}}{4}
\\\\ 最小値：　 -&\frac{3\sqrt{3}}{4}\end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。