中学数学の「一次関数と図形」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年9月2日2023年1月13日中学数学実用数学技能検定（数学検定 数検),数検3級

[mathjax]

問題

\( \ xy \ \)平面上に\( \ \triangle \mathrm{DBE} \ \)がある。
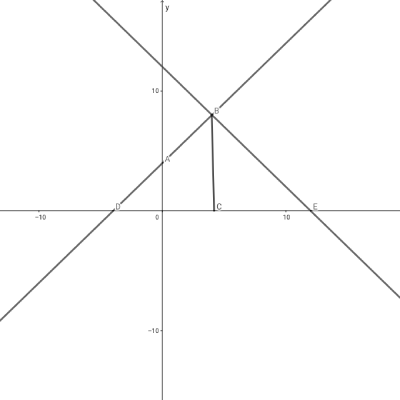
この\( \ \triangle \mathrm{DBE} \ \)は、\( \ \mathrm{BD}=\mathrm{BE} \ \)の直角二等辺三角形であるとする。
また、直線\( \ \mathrm{DB} \ \)は、\( \ y=x+4 \ \)で表される。
さらに、点\( \ \mathrm{B} \ \)からおろした垂線と\( \ x \ \)軸との交点を点\( \ \mathrm{C} \ \)とする。

四角形\( \ \mathrm{OABC} \ \)の面積が\( \ 24 \ \)であるとき、点\( \ \mathrm{E} \ \)の座標を求めよ。

わかっていることを書き出してみる。

Lukia

直線\( \ \mathrm{DA} \ \)から点\( \ \mathrm{A} \ \)と点\( \ D \ \)の座標がわかりますね。

$$\begin{align}点\mathrm{A}は&y=x+4\quad の切片であるから \\\\ \mathrm{A}&\left( 0 \ , \ 4\right) \\\\ \\\\ 点\mathrm{D}の&x \ 座標を \ d \ とすると\\\\ &0=d+4\\\\ d=&-4\\\\ \mathrm{D}&\left( -4 \ , \ 0\right) \end{align}$$

台形の面積の公式を使おう。

Lukia

直線\( \ y=x+4 \ \)によって、点\( \ \mathrm{A} \ \)と点\( \ \mathrm{D} \ \)の座標がわかったので、次に台形の面積公式を用いて、点\( \ \mathrm{B} \ \)と点\( \ \mathrm{C} \ \)を求めていきます。

$$\begin{align} 点\mathrm{B} \ の&x座標を \ b \ とおく. \\\\ \mathrm{B}&\left( b \ , \ b+4\right)\quad と表せる.\\\\ また \ \mathrm{C}&\left( b \ , \ 0\right) \quad である。 \end{align}$$
$$\begin{align}四角形\mathrm{OABC}の&面積を \ \mathrm{S} \ とする。 \\\\ \mathrm{S}=&\frac{1}{2}\left( \mathrm{AO}+\mathrm{BC}\right)\times \mathrm{CO} \\\\ =&\frac{1}{2}\left( 4+b+4\right)\times b=24\\\\ &b^2+8b-48=0\\\\ &\left( b+12\right)\left( b-4\right)=0 \\\\ b=&-12 \ , \ b=4\\\\ \\\\ ただし、&図より \ b \gt 0 \ であるので\\\\ b=&4\\\\ \\\\ \mathrm{B}&\left( 4 \ , \ 8\right) \\\\ \mathrm{C}&\left( 4 \ , \ 0\right) \end{align}$$

二直線が垂直に交わるときの傾きの積は？

Lukia

残すは点\( \ \mathrm{E} \ \)となりました。
この点\( \ \mathrm{E} \ \)の座標を求めるやり方は、式から攻めるルートと図形として攻めるルートがあると思います。
まずは、式から攻めるルートを書いてみます。

Lukia

式から攻めるルートの場合、点\( \ \mathrm{B} \ \)の座標と、直線\( \ \mathrm{DA} \ \)の傾きが必要になります。

$$\begin{align}直線\mathrm{BE}&の切片を \ t \ とする。 \\\\ \triangle \mathrm{DBE}が&\mathrm{BD}=\mathrm{BE}の直角二等辺三角形であることより、 \\\\ 直線\mathrm{BE}&の傾きは、-1である.\\\\ y=&-x+t \ は点\mathrm{B}を通るから\\\\ 8=&-4+t\\\\ t=&12\\\\ y=&-x+12 \end{align}$$
$$\begin{align}点\mathrm{E}&のx座標を \ e \ とする.\\\\ 点\mathrm{E}は&直線\mathrm{BE}とx軸との交点であるので \\\\ 0=&-e+12 \\\\ e=&12 \\\\ \mathrm{E}&\left( 12 \ , \ 0\right) \end{align}$$

三角形の合同を用いる

Lukia

私は最初、\( \ \triangle \mathrm{BCD} \ \)と\( \ \triangle \mathrm{BCE} \ \)を用いて、点\( \ \mathrm{E} \ \)の座標を求めたのですが、高校入試の場合は、きちんと合同を証明することまで求められる可能性があるので、めんどくさいというか、ちょっと時間をロスしてしまうかもしれません。

$$\begin{align}\triangle \mathrm{BCD}と&\triangle \mathrm{BCE}において \\\\ \mathrm{BD}=&\mathrm{BE} \\\\ \mathrm{BC}=&\mathrm{BC}\\\\ \angle \mathrm{DBC}=&\angle \mathrm{EBC}\quad より\\\\ &二辺とその挟角がそれぞれ等しいので,\quad \triangle \mathrm{BCD} \equiv \triangle \mathrm{BCE} \end{align}$$
$$\begin{align}辺\mathrm{CD}&の長さは \ 4-\left( -4\right)=8 \\\\ 辺\mathrm{EC}の&長さも8 \ であるので \\\\ 8=&e-4\\\\ e=&12\\\\ \mathrm{E}&\left( 12 \ , \ 0\right) \end{align}$$

こたえ

$$\mathrm{E}\left( 12 \ , \ 0\right)$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。