高校数学の「箱ひげ図からデータを推定する」問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
下はその箱ひげ図である。表の\( \ a \ , \ b \ , \ c \ , \ d \ \)をうめよ。
ただし,\( \ a \ , \ b \ , \ c \ , \ d \ \)はこの順に点数が高いものから並んでいるとする。なお、箱ひげ図中にある点は、平均値の\( \ 61 \ \)点を表すものとする。
| 出席番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 点数 | $$56$$ | $$59$$ | $$a$$ | $$b$$ | $$76$$ | $$c$$ | $$52$$ | $$83$$ | $$46$$ | $$d$$ |
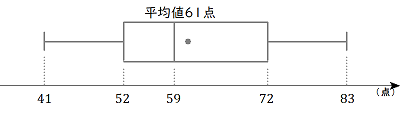
出席番号8の生徒と、出席番号9の生徒の偏差値は、それぞれいくつか。
小数第二位を四捨五入し、小数第一位まで答えよ。
10人を4等分する。
箱ひげ図を理解するには、左から第一、第二、第三とならぶ四分位数を割り出す必要があります。
箱ひげ図の41から52の区画、52から59の区画、59から72の区画、72から83の区画に、
人数が等しくなるように割り振っていきたいのですが、
単純に
$$10\div4=2.5$$
とはできませんよね。
（人間を半分に割るなんて、そんな恐ろしい・・・）
そこで、合同式を用いて、簡単には割り当てられない、余ってしまった人を四分位数に割り当てていきます。
$${10} \equiv {2} \pmod {4}$$
10人を4で割ると、2人が余ってしまいます。
その2人をそれぞれ第一四分位数、第三四分位数に割り当てます。
Lukia
もし、この箱ひげ図が出席番号9番までの9人で作られたものだったとしたら、
\( \ {9} \equiv {1} \pmod {4} \ \) なので、余った1人が第二四分位数に割り当てられます。また、もし、この箱ひげ図が出席番号11番までの11人で作られたものだったとしたら、
\( \ {11} \equiv {3} \pmod {4} \ \) なので、余った3人が、
第一、第二、第三四分位数に割り当てられます。
箱ひげ図と10人の割り振りを図に描きなおすと以下のようになります。
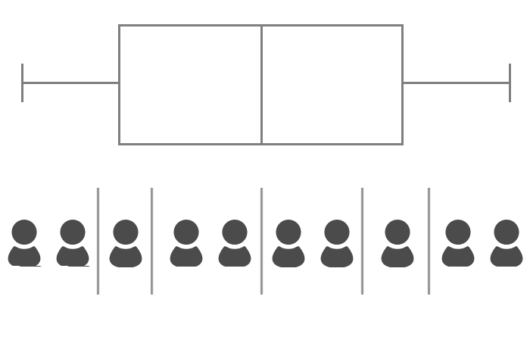（人形アイコンは、ICOOON MONOさんよりいただきました。ありがとうございます。）
この図の人を点数の低いほうからA , B , ・・・J とし、箱ひげ図に書いてあった点数を書き込んだのが、
以下の図です。
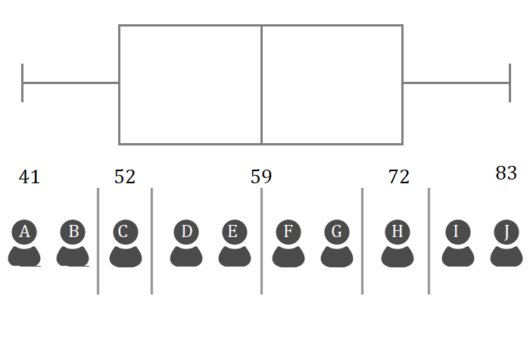箱ひげ図の情報だけで、
Aが41点、
Cが52点、
Hが72点
Jが83点とわかりますね。
次に点数表の数字を書き込んでみます。
対応させてみると、Aの41点にあたる数字が文字に置き換えられているとわかりますね。
$$a \gt b \gt c \gt d$$
という仮定がありましたから、
$$d=41$$
であるといえます。
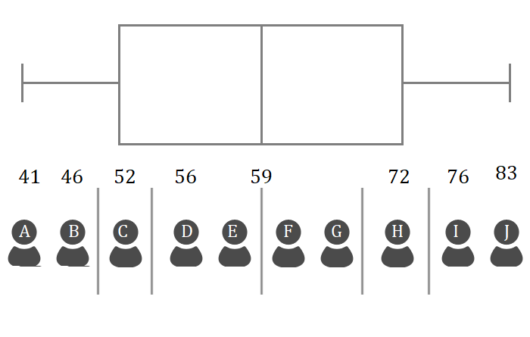Bが46点、
Dが56点
Iが76点とわかります。
59点の人がいない？
箱ひげ図と、点数順に人を並べた図を比べてみると、
第二四分位数である59点に該当する人がいないことになっていますよね。
第二四分位数は、実はEとFの平均点となります。
$$\frac{\mathrm{E}+\mathrm{F}}{2}=59$$
ということですから、
EもFも59点ということになります。
箱ひげ図と点数表をつきあわせてみる。
以下の表は、人形アイコンを挟んで、上の数字が、箱ひげ図からわかったもの、
下の青い枠で囲まれた数字や、青い文字が、点数表からわかったものです。
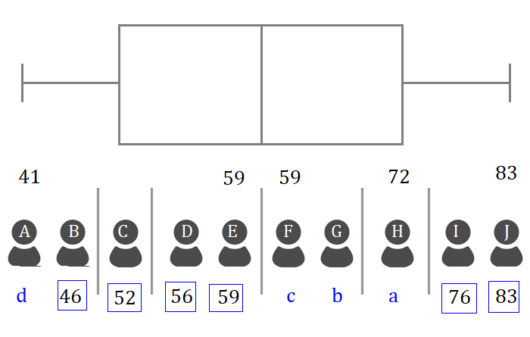上下の数字や文字を対応させてみると、
$$\begin{align}a=&72 \ c=&59 \ d=&41 \end{align}$$
とわかるのですが、
Gの点数であるbが何点なのかわかりません。
ここで、いよいよ平均値の61点を用いて、Gの点数を推定していきます。
10人の偏差の和は0になるはずなので、
$$\begin{align}0=&\frac{1}{10}\sum_{i=1}^{10}{\left( x_i-\overline{x}\right)} \\\\ =&\frac{1}{10}\sum_{i=1}^{10}{\left( x_i-61\right)} \\\\ =&\frac{1}{10}\left( -20-15-9-5-2-2+b-61+11+15+22\right)\\\\ 0=&b-66\\\\ b=&66 \end{align}$$
偏差値を求めてみよう。
細かい説明は、別の機会として、偏差値を求めてみましょう。
$$\begin{align}出席番号 \ をi \ , &点数を \ x_i \ , \\\\ 平均を \ , \ \overline{x} \ , \ \ 標準偏差を& \ s \ , \\\\ 偏差値を\mathrm{DS}_i \ とする.\\\\ \mathrm{DS}_i=&\frac{10\left( x_i-\overline{x}\right)}{s}+50 \end{align}$$
$$\begin{align}\mathrm{DS}_8=&\frac{10\left( 83-61\right)}{12.6}+50=67.46 \sim 67.5 \\\\ \mathrm{DS}_9=&\frac{10\left( 46-61\right)}{12.6}+50=38.09 \sim 38.1\end{align}$$
こたえ
$$a=72 \ , \ b=66 \ , \ c=59 \ , \ d=41$$
$$出席番号8の偏差値：\quad 67.5$$
$$出席番号9の偏差値：\quad 38.1$$
共有:
プロフィール
