高校数学の「二つの実数と絶対値を含んだ定積分」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
$$\mathrm{I}=\int_{0}^{1} \vert \left( x-a\right)\left( x-b\right) \vert dx$$
とおく.
実数\( \ a \ , \ b \ \)の値が変化することによって,\( \ \mathrm{I} \ \)は何通り考えられるか。
どうせ二兎追わねばならぬなら？
ディノ
Lukia
ディノ
Lukia
ディノ
Lukia
何通りあるのか。を考えなくてはならないので、そこがちょっと難しいですよね。
ここで、ディノさんに質問です。
「二兎追う者は一兎をも得ず。」ということわざがありますが、
ウサギ小屋に二羽のウサギがいたとして、そのウサギを捕まえなくてはならないとき、ディノさんなら、どうしますか？
ディノ
だとしたら、ひとまず、一羽を捕まえることに集中して、そのあともう一羽を捕まえるかな。
Lukia
そして、\( \ 0 \ \)以上\( \ 1 \ \)以下というのが、いわばウサギ小屋ですね。
ディノ
フフフフ・・・。（￣ー￣）
Lukia
ウサギaの位置を考える。
Lukia
\( \ 0 \leq a \leq 1 \ \)として、どんな場合が考えられますか？
ディノ
\( \ 0 \lt a \lt 1 \ \)と、
\( \ a=1 \ \)だな。
Lukia
二羽のウサギの間には、\( \ a \leq b \ \)という関係が成り立っていますね。
ウサギ\( \ a \ \)は、ウサギ\( \ b \ \)より小さいか、全く同じ大きさか。
ウサギ\( \ a \ \)の位置を決めてやらなければ、ウサギ\( \ b \ \)の位置を定めるのは難しいですよね。
Lukia
Ⅰ \( \ a=0 \ \)
Ⅱ \( \ 0 \lt a \lt 1 \ \)
Ⅲ \( \ a=1 \ \) としましょう。
ウサギbの位置を考える。
Lukia
ディノ
ウサギ\( \ a \ \)と\( \ 1 \ \)に挟まれる。って感じだよな。
じゃ、\( \ a \leq b \leq 1 \ \)かな？
Lukia
ⅰ \( \ a=b \ \)
ⅱ \( \ a \lt b \lt 1 \ \)
ⅲ \( \ b=1 \ \) と考えられますね。
ディノ
ウサギ\( \ b \ \)が3通りだから、
\( \ 3\times 3=9 \ \) で、9通りか？
Lukia
Iを考える。
$$\begin{align}Ⅰ\quad \quad &a=0\quad について, \\\\ &ⅰ\quad a=b \\\\ &ⅱ\quad a \lt b \lt 1\\\\ &ⅲ\quad b=1\quad を考える. \end{align}$$
Ⅰ-ⅰ
$$\begin{align}a=b=0&\quad より, \\\\ \mathrm{I}_1=&\int_{0}^{1} x^2 dx \end{align}$$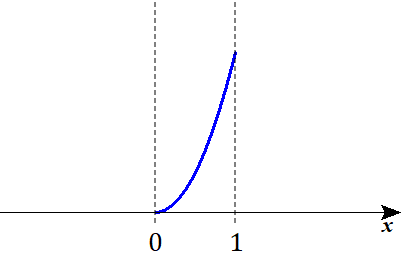 
Ⅰ-ⅱ
$$\begin{align}a=0 \ ,&a \lt b \lt 1\quad より, \\\\ \mathrm{I}_2=&\int_{0}^{1} \vert x\left( x-b\right) \vert dx \end{align}$$
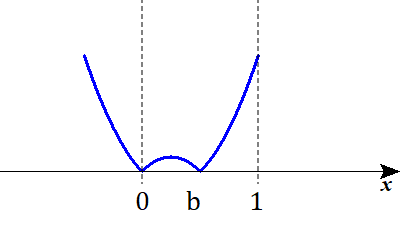
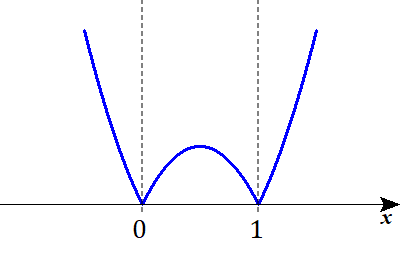
Ⅰ-ⅲ
$$\begin{align}a=0 \ ,&b=1\quad より, \\\\ \mathrm{I}_3=&\int_{0}^{1} \vert x\left( x-1\right) \vert dx \end{align}$$
Ⅱを考える。
$$\begin{align}Ⅱ\quad \quad &0 \lt a \lt 1\quad について, \\\\ &ⅰ\quad a=b \\\\ &ⅱ\quad a \lt b \lt 1\\\\ &ⅲ\quad b=1\quad を考える. \end{align}$$
Ⅱ-ⅰ
$$\begin{align}0 \lt a=b \lt 1&\quad より, \\\\ \mathrm{I}_4=&\int_{0}^{1} \left( x-a\right)^2 dx \end{align}$$
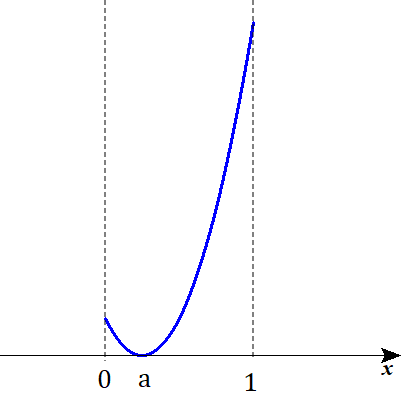
Ⅱ-ⅱ
$$\begin{align}0 \lt a \lt b \lt 1&\quad より, \\\\ \mathrm{I}_5=&\int_{0}^{1} \vert \left( x-a\right)\left( x-b\right) \vert dx \end{align}$$
Ⅱ-ⅲ
$$\begin{align}0 \lt a \lt 1 \ ,&b=1\quad より, \\\\ \mathrm{I}_6=&\int_{0}^{1} \vert \left( x-a\right)\left( x-1\right) \vert dx \end{align}$$
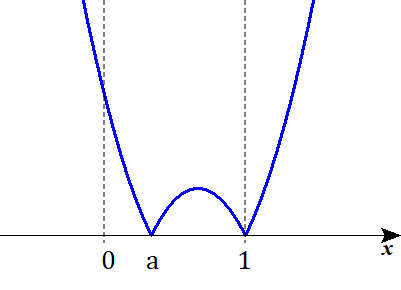
Ⅲを考える。
$$\begin{align}Ⅲ\quad \quad &0 \lt a \lt 1\quad について, \\\\ &ⅰ\quad a=b \\\\ &ⅱ\quad a \lt b \lt 1\\\\ &ⅲ\quad b=1\quad を考える. \end{align}$$
Ⅲ-ⅰ
$$\begin{align}a=b=1&\quad より, \\\\ \mathrm{I}_7=&\int_{0}^{1} \left( x-1\right)^2 dx \end{align}$$
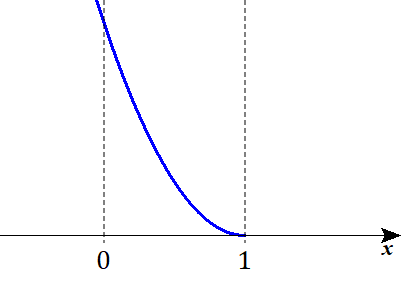
Ⅲ-ⅱ
$$\begin{align}a=1 \lt b \lt 1&\quad は範囲に矛盾があるため,\quad 不適. \end{align}$$
Ⅲ-ⅲ
$$\begin{align}a=b=1&\quad は,\quad Ⅲ-ⅰ\quad に同じ。\end{align}$$
Ⅰ～Ⅲをまとめる。
$$\begin{align}Ⅰ～Ⅲより,& \\\\ 定積分 \ \mathrm{I}&\quad は\quad 7 \ 通り考えられる。\end{align}$$
こたえ
7通り
共有:
プロフィール
