高校数学の「微分とその応用（極値・変曲点を求める）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月21日2023年1月14日微分とその応用実用数学技能検定（数学検定数検),数検準1級

読了時間: 約6分2秒

問題

次の曲線の変曲点の座標をすべて求めよ。
$ \ y=x+2\sin x\quad \left( -\frac{ \pi }{ 2 } \lt x \lt {\frac{ 3 }{ 2 }}\pi\right) \ $

変曲点を求めるには。

Lukia

$ \ y=f\left( x\right) \ $とみなしたとき、
一回微分した$ \ ｆ’\left( x\right) \ $で極値が求められます。
そして、$ \ f’\left( x\right) \ $を微分した（元の$ \ f\left( x\right) \ $を2回微分）$ \ f″\left( x\right) \ $によって変曲点が求められます。

Lukia

今回は、変曲点を求めるだけでなく、グラフも描いてみましょう。

$$\begin{align}y=&f\left( x\right)\quad とする. \\\\ f’\left( x\right)=&1+2\cos x \\\\ f″\left( x\right)=&-2\sin x \end{align}$$
極値を求める.
$$\begin{align}f’\left( x\right)=&1+2\cos x=0 \\\\ \cos x=&-\frac{1}{2} \\\\ x=&{\frac{ 2 }{ 3 }}\pi\quad ,\quad {\frac{ 4 }{ 3 }}\pi \end{align}$$
変曲点を求める.
$$\begin{align}f″\left( x\right)=&-2\sin x=0 \\\\ \sin x=&0 \\\\ x=&0\quad ,\quad \pi \end{align}$$
ゆえに変曲点の座標は,
$$\left( 0\quad ,\quad 0\right)\quad \left( \pi\quad ,\quad \pi\right)$$

Lukia

いかがですか?
この問題自体は、さほど難しくないですね。
しかし、$ \ y=k \ $と3つの共有点をもつ定数$ \ k \ $の値の範囲を求めよ.
なんて問題があったら、グラフが描けないと解けないですよね。
というわけで、グラフ、増減表を描いて元のグラフを描いてみます。

一回微分した式のグラフを描いてみる。

$$\begin{align}f’\left( x\right)=&1+2\cos x\quad のグラフは, \\\\ y=&\cos x\quad のグラフを \ y \ 軸方向に2倍に拡大し, \\\\ y& \ 軸方向に1平行移動させたもの. \end{align}$$

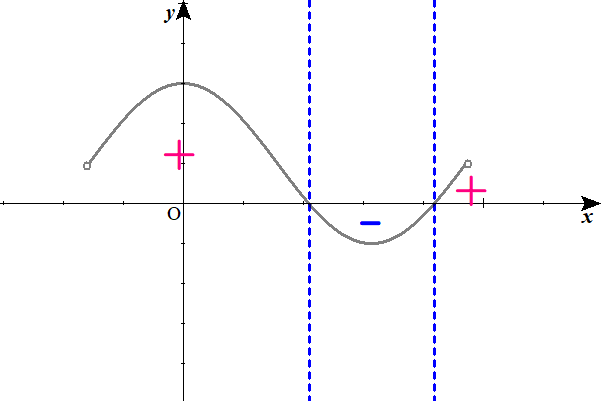
二回微分した式のグラフも描いてみる。

$$\begin{align}f″″\left( x\right)=&-2\sin x\quad は, \\\\ y=&\sin x\quad のグラフを \ y \ 軸方向に-2倍に拡大したもの.\end{align}$$

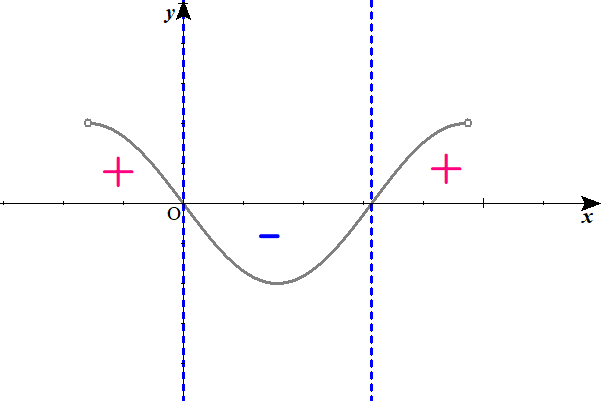
増減表をかく。

Lukia

二つのグラフを元に,増減表をかいていきます。

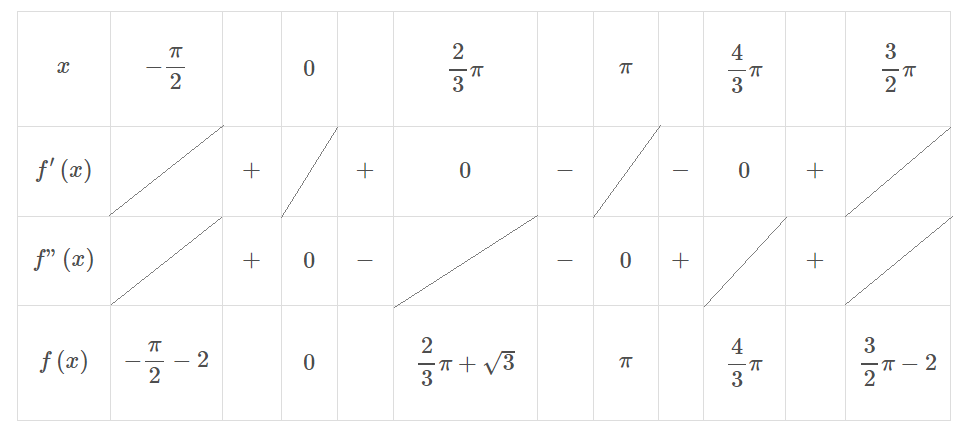
より正確なグラフを描くために。

Lukia

上の増減表で、$ \ f’\left( x\right) \ $と$ \ f″\left( x\right) \ $の段に$ \ + \ $や$ \ – \ $の記号が書かれていますね。
数学ⅡBレベルであれば、一回微分をして、極値を求め、その座標をめがけてなんとなく凹凸がついた曲線を描いていましたが、
せっかく二回微分をして、変曲点を求めたのですから、より正確な凹凸のグラフを描いてみましょう。

Lukia

$ \ + \ $と$ \ – \ $の組合せは、全部で4通りありますね。
まず、$ \ f’\left( x\right) \ $の段にある$ \ + \ $と$ \ – \ $は、$ \ xy \ $平面において、曲線が右に移動するにつれ、上昇するのか下降するのかを示しています。
そして、$ \ f″\left( x\right) \ $の段にある$ \ + \ $と$ \ – \ $は、曲線の凸の方向を示しています。

	わかること	例1	例2	例3	例4
$$f’\left( x\right)$$	上昇か下降か	+	+	–	–
$$f’\left( x\right)$$	上昇か下降か	上昇	上昇	下降	下降
$$f″\left( x\right)$$	凸の方向	+	–	+	–
$$f″\left( x\right)$$	凸の方向	下に凸	上に凸	下に凸	上に凸
$$f\left( x\right)$$	曲線

Lukia

増減表自体は、数学ⅡB範囲でもかいていたので、上昇と下降の矢印の向きは、問題なく書き込めると思いますが、
覚えにくいのは、凸の方向ではないでしょうか。
私は、つい先ほどまで、
「（上昇・下降の）矢印は、柔らかい素材でできていて、どちらの方向から力がかかるか」と覚えていました。
例えば、上の表の「例1」だと、柔らかい素材でできた矢印は、上昇の方向を指しています。
しかし、上から$ \ + \ $に乗っかられたので、その重さで矢印はたわみ、下に凸の上昇矢印となったと考えます。
また、「例2」の場合は、上昇の矢印が、下から$ \ – \ $にもぐりこまれたので、そのぶん上にたわみ、上に凸の上昇矢印になったと考えていました。

Lukia

曲線の凹凸の方向の覚え方は、人それぞれ合うものがあると思いますので、自分でも探してみるといいと思います。

ここで、「上に凸、下に凸」というと、いわゆる二次関数でよく目にする言葉ですよね。
$ \ y=ax^2+bx+c \quad \left( a \ , \ b \ , \ c\quad はいずれも実数,特に \ a \neq 0\right)\ $において、
$ \ a \gt 0 \ $（すなわち正）のとき、下に凸の関数でしたし、
$ \ a \lt 0 \ $（すなわち負）のとき、上に凸の関数でした。

Lukia

これだと、二次関数の凸の方向と紐付けされているので、
度忘れしたり、悩んだときに、二次関数の凸の方向を思い出せばいいことになりますから、確実に思い出せそうでいいですね。
（私も、今日から、これにします。）

Lukia

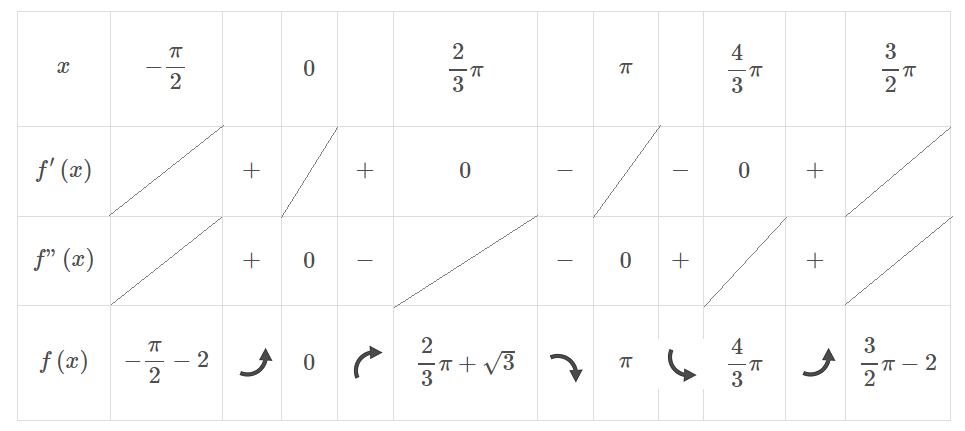
さて、グラフの上昇・下降と凸の方向を書き込んだ増減表は以下の通りです。

大小関係さえ正確ならば目盛りの幅は気にしなくていい。

Lukia

さて、いよいよグラフを描いていくわけですが、その際に必要となるのが、$ \ f\left( x\right) \ $の値ですね。

$ \ f\left( x\right) \ $の値は、だ～いたいでいいです。
この記事のグラフは、GRAPES（グレープス）という数学のグラフ描画ソフトを用いて描いているので、正確です。
しかし、実際の大学入試では、グラフ描画ソフトなんて使えませんし、値そのものは正確でなくても、大小関係さえ正確であればなんとか答えが出るようにしてあります。
記事にするまえに、増減表をもとにグラフを手描きしたのですが、いわゆる$ \ y \ $軸の目盛りの幅は大変いい加減です。
でも、$ \ y=k \ $との共有点の数を求める場合は、かえって目盛りがデフォルメされたほうがわかりやすいこともあります。
私は、今回、$ \ \pi \sim 3 \ $とし、$ \ \sqrt{3} \sim 1.7 \ $として計算してだいたいの値を求めておき、
値の大小関係だけは正確な目盛りを打って、グラフを描きました。
それが以下の写真の図です。

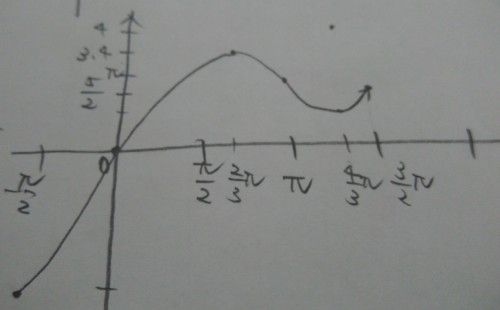
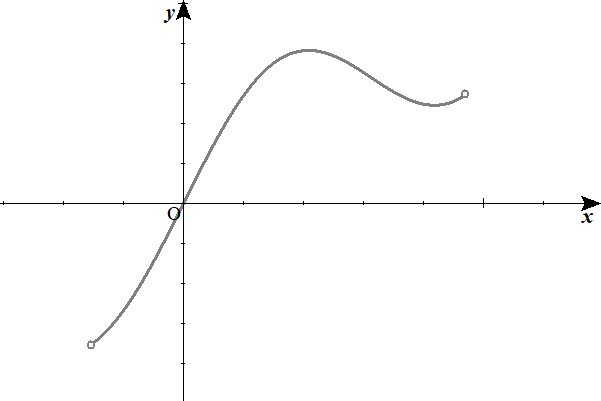
Lukia

そして、上のグラフが、GRAPES（グレープス）で描いた曲線です。
$ \ y \ $軸の目盛りの幅は、全然正確ではないのに、ほぼ似たような曲線が描けていますね。

Lukia

数学Ⅲの範囲であるとか、大学の二次試験の問題ともなってくると、
グラフに関しては、目盛りの正確さよりも、値の大小関係の正確さが求められます。
（幾何の問題は、正確な方がよさそうですけどね）
もちろん、正確な値でグラフが描ければよいのですが、$ \ y=e^x \ $のグラフなんて、正確に描いていたら、紙面がいくらあっても足りません。
出題者は、グラフの概形が描けること、それを参考にして、さらなる問題を解くことができるかどうかが知りたいのですから、他の受験生と差をつけるには、増減表を作る、それを元にグラフの概形を描く。という一連の作業をいかに短時間でこなせるか。にかかっています。
解答集にグラフが描かれているような問題は、たとえグラフを描くことを求められていなくても、練習のため、描いてみることをオススメします。