高校数学の「放物線と直線で作られる三角形の面積」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月24日2023年1月14日中学数学,二次関数実用数学技能検定（数学検定数検),数検3級,数検準2級

読了時間: 約9分51秒

[mathjax]

問題

図のように、放物線$ \ y=\frac{1}{2}x^2 \ $と直線 $ \ y=-x+4 \ $が2点 $ \ \mathrm{A} \ , \ \mathrm{B} \ $で交わるとする.

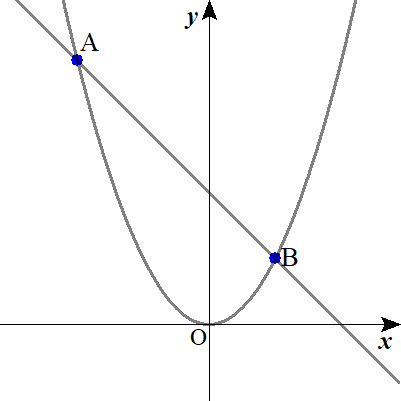
ここで放物線上に点$ \ \mathrm{C} \ \left( c \ , \ \frac{1}{2}c^2\right) \ $$ \ \left( -4 \lt c \lt 0\right) \ $をとる.
$ \ \triangle \mathrm{ABO} \ $と$ \ \triangle \mathrm{ABC} \ $の面積が等しくなるときの$ \ c \ $の値を求めよ.

Lukia

Yahoo!知恵袋に載っていた問題はもっと長かったのですが、カットさせていただきました。
タイトルに「高校数学の」とつけていますが、$ \ \triangle \mathrm{ABO} \ $の面積を求めるのは、高校入試でもよく出題されていますので、
高校生以上は、知っている、確実に解けるという状態であってほしい問題です。

2点A,Bの座標を求めておく。

放物線と直線の交点 A , Bは
$$\begin{align}\frac{1}{2}x^2=&-x+4 \\\\ x^2+2x-8=&0 \\\\ \left( x+4\right)\left( x-2\right)=&0\\\\ x=-4 \ &, \ x=2 \end{align}$$
図より
$$\begin{align}点\mathrm{A}& \ \left( -4 \ , \ 8\right) \\\\ 点\mathrm{B}& \ \left( 2 \ , \ 2\right) \end{align}$$

Lukia

2点の座標が明らかになったところで、
いよいよ三角形の面積を求めていきます。
まずは、$ \ \triangle \mathrm{ABO} \ $の面積がいったいいくらなのかをわかっておかなければ$ \ c \ $に関する方程式が解けそうにありませんね。

Lukia

求める$ \ \triangle \mathrm{ABO} \ $は上の図の薄紫で塗りつぶされた三角形です。
この三角形の面積は、小学校の算数で習った公式をあてはめれば楽に求められます。

もも

$ \ 底辺 \ \times \ 高さ \ \div \ 2 \ $です！

Lukia

も、ももちゃん・・・。
久しぶりですね。
（ももちゃんは、中学生のペルソナです）

もも

最近、出番がないんですもん。

Lukia

そうでしたね。
それでは、お手伝いしてもらいましょうかね。

高校数学における作図のデフォルトは「フリーハンド」です。

Lukia

小学校で習った三角形の面積の公式は、底辺と高さが必ず「直角に」交わっているのが大前提でした。
しかし、この薄紫色の三角形の面積を求めるうえで、仮に「底辺は辺$ \ \mathrm{AB} \ $だ！」と思ってしまった場合、高さはどうやって求めたらいいでしょう。

もも

う～ん、分度器の直線部分を辺$ \ \mathrm{AB} \ $にあて、
分度器の$ \ 90^{\circ} \ $を示す直線が点$ \ \mathrm{O} \ $を通るようにして、印をつけておいてから、
辺$ \ \mathrm{AB} \ $の長さと、点$ \ \mathrm{O} \ $から辺$ \ \mathrm{AB} \ $におろした垂線の長さをはかりますかねぇ。

Lukia

いくつかの条件が調っていれば、そうなるでしょうねぇ。

もも

条件？

Lukia

まず、定規・分度器・コンパスなどの使用が許可されていること。
図がかなり正確に描かれていること。
放物線と直線は、解答者が描くような問題であっても、解答用紙にかなり正確なグラフ用紙が載っていること。
はたまた、辺$ \ \mathrm{AB} \ $や点$ \ \mathrm{O} \ $から引いた垂線が、かなりキリのいい長さであること。

Lukia

このように、解答者に優しい至れり尽くせりの問題であればいいですが、入試問題や、高校数学レベルではそうはいきません。

たとえば、先日行われた大学入試センター試験などは、試験中に結構な図を描かせますが、定規やコンパスの持ち込みは不可です。
持ち込めば不正行為とみなされます。

もも

そ、そんな厳しいんですか。

Lukia

はい。
ですから、高校数学では、グラフは「フリーハンド」で描き、なるべく精度を上げる練習をしておくとよいですね。
まっすぐな線が引けるとか、一定の目盛りが打てるとか。
円が描けるようにしておくのもポイントが高いと思います。精度を高めたとはいえ、「フリーハンド」で描くのですから、正確な値は計算によって求めるのが大前提となります。
つまり、図は、計算式を導きだすまでの補助的なもので、正確さは問わない、問えないと思っていたほうがいいですね。

もも

ということは、今回の問題では、「分度器や定規などを使わなくても、三角形の面積は求められる。」ということですね。

Lukia

相変わらず、勘が鋭いですねぇ。
そうです、その通りです。
この$ \ xy \ $平面上で、確実に・・・垂直に交わっている線があるのですが、わかりますか？

もも

えっと・・・
$ \ x \ $軸と$ \ y \ $軸かな？

Lukia

そのとおりです！
図では省略していますが、それぞれの軸に平行になるように$ \ x=1, \ 2, \ 3, \ \cdots \ $とか、$ \ y=1, \ 2, \ 3, \ \cdots \ $のように細かく線を引くことができますね。

Lukia

今回は、新しい視点を得て、三角形の面積を求めていきましょう。

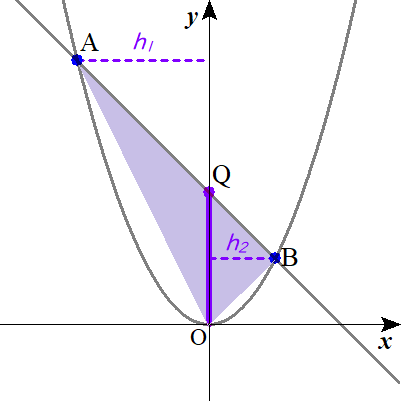
2つの三角形の和と考える。

Lukia

今回、底辺を辺$ \ \mathrm{OQ} \ $とします。
ちなみに、点Qは直線の切片にあたりますから、辺$ \ \mathrm{OQ} \ $の長さは・・・

もも

4です。

Lukia

そうですね。
さらに、$ \ \triangle \mathrm{ABO}=\triangle \mathrm{AOQ}+\triangle \mathrm{BOQ} \ $とします。
$ \ \triangle \mathrm{AOQ} \ $または、$ \ \triangle \mathrm{BOQ} \ $の高さは、点A、点Bからそれぞれ$ \ y \ $軸におろした垂線$ \ h_1 \ , \ h_2 \ $にあたりますね。

Lukia

垂線（高さ）$ \ h_1 \ , \ h_2 \ $のそれぞれの長さはわかりますか？

もも

点$ \ \mathrm{A} \ $を通り、$ \ x \ $軸と平行になる直線が$ \ y \ $軸と交わる点を$ \ \mathrm{A’} \ $とすると・・・。
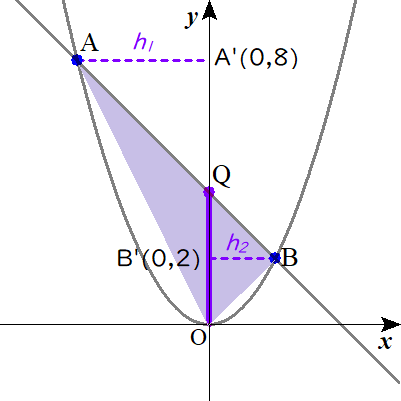
点$ \ \mathrm{A’} \ $は、$ \ \left( 0 \ , \ 8\right) \ $です。

もも

ということは、点$ \ \mathrm{A} \ $と点$ \ \mathrm{A’} \ $の$ \ x \ $座標の値の差が$ \ h_1 \ $の長さにあたります！

もも

だから、$ \ h_1=x_{\mathrm{A’}}-x_\mathrm{A}=0-\left( -4\right)=4 \ $

もも

辺$ \ \mathrm{BB’} \ $の方も同じようにやればいいから、
$ \ h_2=x_\mathrm{B}-x_{\mathrm{B’}}=2-0=2 \ $以上、二つの三角形のそれぞれの高さが求められました。

$$\begin{align}\triangle \mathrm{ABO}=&\triangle \mathrm{AOQ}+\triangle \mathrm{BOQ} \\\\ =&\frac{1}{2}\mathrm{OQ}\cdot h_1+\frac{1}{2}\mathrm{OQ}\cdot h_2 \\\\ =&\frac{1}{2}\mathrm{OQ}\left( h_1+h_2\right) \\\\ =&\frac{1}{2}\cdot 4\left( 4+2\right)\\\\ =&12 \end{align}$$

もも

おお～、計算できた～。

Lukia

ここまでの問題は、高校入試でも出題されます。
底辺というと、両目と平行になるように引かれていることが多かったと思いますが、
視点を$ \ 90^{\circ} \ $回転させ、さらに両側に「高さ」を広げた三角形を読み取らなければならないので、一度はやっておかないと気づけない問題かもしれませんね。

ふたつの三角形に共通しているのは？

Lukia

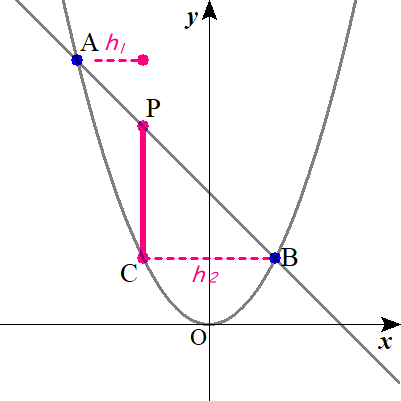
それでは、$ \ \triangle \mathrm{ABC} \ $の面積も求めていきましょう。
図は、以下のようになり、ピンクで塗りつぶされた三角形の面積を求めることになりますね。

もも

ということは、底辺を、辺$ \ \mathrm{CP} \ $とすると、
$ \ \triangle \mathrm{ABC} \ $は、$ \ \triangle \mathrm{ACP} \ $と$ \ \triangle \mathrm{BCP} \ $に分割され、
それぞれの三角形の高さは、2点$ \ \mathrm{A} \ , \ \mathrm{B} \ $から辺$ \ \mathrm{CP} \ $に引いた垂線の長さとなりますね。

Lukia

ちなみに、点$ \ \mathrm{P} \ $の座標はわかりますか？

もも

点$ \ \mathrm{P} \ $の$ \ x \ $座標は、点$ \ \mathrm{C} \ $のそれと共通しているから・・・
直線の式に代入して、$ \ y=-c+4 \ $とわかるから、
$ \ \mathrm{P} \ \left( c \ , \ -c+4\right) \ $です。

Lukia

おお～、いいですねぇ。
それでは、$ \ \triangle \mathrm{ABO} \ $の面積の求め方を参考に式を立ててもらえますか？

もも

がんばってみます！

$$\begin{align}\triangle \mathrm{ABC}=&\triangle \mathrm{ACP}+\triangle \mathrm{BCP} \\\\ =&\frac{1}{2}\mathrm{CP}\cdot h_1+\frac{1}{2}\mathrm{CP}\cdot h_2 \\\\ =&\frac{1}{2}\mathrm{CP}\left( h_1+h_2\right) \end{align}$$

もも

えっと・・・
辺$ \ \mathrm{CP} \ $の長さは、$ \ y \ $座標の差で求められるとして・・・
$ \ h_1 \ $と$ \ h_2 \ $は・・・

Lukia

$\triangle \mathrm{ABO}$のときと変わっていますか？

もも

あっ、それぞれの三角形で、$ \ h_1 \ $と$ \ h_2 \ $の長さは違うけど、
$ \ h_1 \ $と$ \ h_2 \ $の和は点$ \ \mathrm{A} \ $と点$ \ \mathrm{B} \ $の$ \ x \ $座標の差に等しいんだから、高さは$ \ \triangle \mathrm{ABO} \ $で求めた$6$のままということですね！

$$\begin{align}\triangle \mathrm{ABC}=&\triangle \mathrm{ACP}+\triangle \mathrm{BCP} \\\\ =&\frac{1}{2}\mathrm{CP}\left( h_1+h_2\right) \\\\ =&\frac{1}{2}\mathrm{CP}\left( x_\mathrm{B}-x_\mathrm{A}\right)\\\\ =&\frac{1}{2}\mathrm{CP}\cdot 6\\\\ =&3\mathrm{CP} \end{align}$$
$$\begin{align}\triangle \mathrm{ABO}=&\triangle \mathrm{ABC} \\\\ 12=&3\mathrm{CP} \\\\ 4=&y_\mathrm{P}-y_\mathrm{C} \\\\ 4=&-c+4-\frac{1}{2}c^2 \\\\ c^2+2c=&0\\\\ &c=-2 \ , \ 0\ \\\\ ただし,&-4 \lt c \lt 0\quad より\\\\ c=&-2 \end{align}$$

図から共通するものを見つけられればもっと楽に解ける。

Lukia

グラフ上に二つの三角形を描き、共通するものが何か（今回は高さが共通）がわかれば、もっと早く、もっと楽に計算にたどりつくことができます。

$$\begin{align}\triangle \mathrm{ABO}=&\triangle \mathrm{ABC} \\\\ \triangle \mathrm{AOQ}+\triangle \mathrm{BOQ}=&\triangle \mathrm{ACP}+\triangle \mathrm{BCP} \\\\ \frac{1}{2}\mathrm{OQ}\left( x_\mathrm{B}-x_\mathrm{A}\right)=&\frac{1}{2}\mathrm{CP} \left( x_\mathrm{B}-x_\mathrm{A}\right)\\\\ \mathrm{OQ}=&\mathrm{CP}\\\\ y_\mathrm{Q}-y_\mathrm{O}=&y_\mathrm{P}-y_\mathrm{C}\\\\ 4=&-c+4-\frac{1}{2}c^2\\\\ \frac{1}{2}c\left( c+2\right)=&0\\\\ -4 \lt &c \lt 0\quad より\\\\ c=&-2 \end{align}$$