高校数学の「定義域が設定された二次関数（放物線）の最大値・最小値」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約3分30秒
[mathjax]
問題
(1) \( \ a \ \)は定数 \( \ 1 \leq a \leq 2 \ \)のとき,
二次関数 \( \ y=x^2-4x\quad \left( a \leq x \leq a+1\right) \ \)の最小値を求めよ.
(2) \( \ a \geq \frac{3}{2} \ \)のとき,二次関数\( \ y=x^2-4x\quad \left( a \leq x \leq a+1\right) \ \)の最大値を\( \ a \ \)を用いて表せ.
二次関数 \( \ y=x^2-4x\quad \left( a \leq x \leq a+1\right) \ \)の最小値を求めよ.
(2) \( \ a \geq \frac{3}{2} \ \)のとき,二次関数\( \ y=x^2-4x\quad \left( a \leq x \leq a+1\right) \ \)の最大値を\( \ a \ \)を用いて表せ.
問題から出題者のメッセージが受け取れる？
Lukia
定義域が設定された最大値・最小値問題は、大学入試センター試験の数学ⅠまたはⅠAでは、常連のような問題ですよね。
問題の後半の方に設定され、ときには結構な高配点だったりするので、できるようになっておきたい、または、そこまで短時間にたどりつくだけの解答スピードを身に着けておきたいものです。
問題の後半の方に設定され、ときには結構な高配点だったりするので、できるようになっておきたい、または、そこまで短時間にたどりつくだけの解答スピードを身に着けておきたいものです。
Lukia
この問題を解いたとき、ちょっとまどろっこしい方法をとったのですが、
解き終わってから、この問題が求めていること、（メッセージ）とは別の方向だったように思いました。
解き終わってから、この問題が求めていること、（メッセージ）とは別の方向だったように思いました。
Lukia
私が思うに、この問題を作成した人（出題者）は、以下のようなことを確かめたいのではないかと思います。
- 解答者に解法の軸というか、ゆるがない方針のようなものがあるか（行き当たりばったりではない）
- 何が求められているか、何ができるようになってほしいか。がどれだけ意識できているか。
Lukia
「数学の問題にメッセージが込められてるなんて、イっちゃってんじゃないの？」と思われそうですが、どんなものでも勉強しているとそれなりのメッセージ性は感じるものです。
最大値・最小値問題で意識するのは、定義域の「中央」
Lukia
話が長くなってしまいましたが、今回の問題で求められているのは、
「定義域の中央が意識できているか。」ということです。
放物線の軸を意識することはいうまでもないことですが、この「定義域の中央」が意識できると、問題が解きやすくなると思います。
「定義域の中央が意識できているか。」ということです。
放物線の軸を意識することはいうまでもないことですが、この「定義域の中央」が意識できると、問題が解きやすくなると思います。
$$\begin{align}定義域の&中央は,\quad \\\\ x=&\frac{a+a+1}{2}=\frac{2a+1}{2} \\\\ 定義域の&中央の存在範囲を求める.\\\\ 1 \leq &a \leq 2\\\\ 2& \leq 2a \leq 4\\\\ 2+1 \leq 2&a+1 \leq 4+1\\\\ \frac{3}{2} \leq &\frac{2a+1}{2} \leq \frac{5}{2}\end{align}$$
Lukia
定義域は、幅1で移動するわけですが、
以下に示す図は、定義域が左右どこまで存在できるか、いわゆるギリを示したものです。
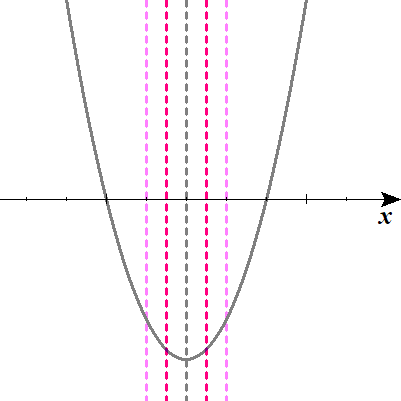
以下に示す図は、定義域が左右どこまで存在できるか、いわゆるギリを示したものです。
Lukia
まず、図の濃いピンクの点線が、上で求めた「定義域の中央」が存在する範囲です。
定義域そのものの幅が1ですので、濃いピンクの点線から\(\frac{1}{2}\)離れたところに、定義域の左端の限界（左限とでもしておきましょう）と、右端の限界（右限）が存在することになります。これを示したのが、淡いピンクの点線ですね。
定義域そのものの幅が1ですので、濃いピンクの点線から\(\frac{1}{2}\)離れたところに、定義域の左端の限界（左限とでもしておきましょう）と、右端の限界（右限）が存在することになります。これを示したのが、淡いピンクの点線ですね。
Lukia
さらに図を見ると、放物線の軸（図では灰色の点線）が定義域の存在範囲に含まれていますね。
つまり、定数\( \ a \ \)が\( \ 1 \leq a \leq 2 \ \)を満たしていれば、最小値は必ず\( \ x=2 \ \)のときに取ることがわかります。
つまり、定数\( \ a \ \)が\( \ 1 \leq a \leq 2 \ \)を満たしていれば、最小値は必ず\( \ x=2 \ \)のときに取ることがわかります。
$$求める最小値は -4\quad \left( \ x=2 \ のとき \ \right) $$
(2)を解く。
定義域の中央を求める.
$$\begin{align}\frac{3}{2} \leq &a \\\\ 3 \leq &2a \\\\ 3+1 \leq &2a+1\\\\ 2 \leq &\frac{2a+1}{2} \end{align}$$
Lukia
下の図を参考にしながら、最大値を求めていきましょう。
図の濃いピンクの点線が、定義域の中央を示します。
さらに淡いピンクの点線が定義域の左限ですね。
濃いピンクの点線が右にスライドするにつれて、定義域も右にスライドしていきます。
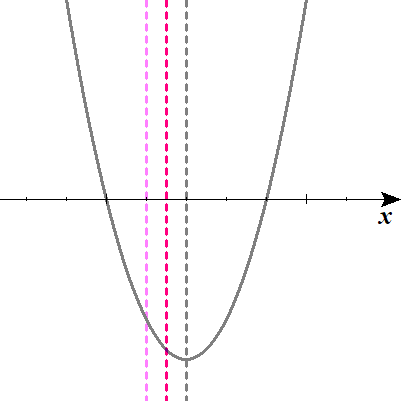
図の濃いピンクの点線が、定義域の中央を示します。
さらに淡いピンクの点線が定義域の左限ですね。
濃いピンクの点線が右にスライドするにつれて、定義域も右にスライドしていきます。
Lukia
\( \ y=x^2-4x \ \)は、下に凸の放物線ですから、軸から離れた定義域の端点が最大値を示します。
Lukia
\( \ a \ \)の値が大きくなるにつれて、定義域は右にスライドするので、最大値は、常に\( \ x=a+1 \ \)のときにとると考えることができます。
$$\begin{align}求める最大値は, \ &x=a+1\quad のとき. \\\\ \mathrm{M}\left( a+1\right)=&\left( a+1\right)^2-4\left( a+1\right) \\\\ =&a^2-2a-3 \end{align}$$
こたえ
$$\begin{align}\left( 1\right)\quad &最小値： \ -4 \\\\ \left( 2\right)\quad &最大値： \ a^2-2a-3\end{align}$$
[subscribe2]
共有:
プロフィール
Author Profile
