高校数学の「曲線と接線」に関する問題を解いてみる。【Yahoo!知恵袋より】

2022年7月20日2023年1月8日微分と積分

Yahoo!知恵袋の高校数学カテゴリに掲載されていた「曲線と接線」に関する問題を解いてみました。

解法

接点の\( \ x \ \)座標を \( \ t \ \) とおく。
ゆえに接点の座標は\( \ \left( t \ , \ t^3-2t^2+1\right) \ \) となる。
接線の方程式は、\( \ y=\left( 3t^2-4t\right)\left( x-t\right)+t^3-2t^2+1 \ \) である。
これが \( \ \mathrm{P}\left( 3 \ , \ 1\right) \ \)を通るから
\( \ -2t^3+11t^2-12t=0 \ \)
\( \ t\left( t-4\right)\left( -2t+3\right)=0 \ \)
\( \ t=0 \ , \ t=4 \ , \ t=\displaystyle\frac{3}{2} \ \)

1) \( \ t=0 \ \) のとき
\( \ y＝1 \ \) 接点は\( \ \mathrm{A}\left( 0 \ , \ 1\right) \ \)

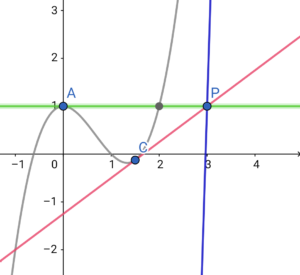
2) \( \ t=4 \ \) のとき
\( \ y＝32x-95 \ \) 接点は\( \ \mathrm{C}\left( 4 \ , \ 33\right) \ \)
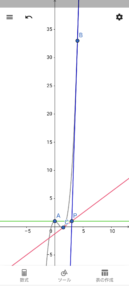3) \( \ t=\displaystyle\frac{3}{2} \ \) のとき
\( \ y＝\displaystyle\frac{3}{4}x-\displaystyle\frac{5}{4} \ \) 接点は\( \ \mathrm{B}\left( \displaystyle\frac{3}{2} \ , \ -\displaystyle\frac{1}{8}\right) \ \)

こたえ

$$\begin{align}y=&1 \\\\ y=&32x-95 \\\\ y=&\frac{3}{4}x-\frac{5}{4} \end{align}$$

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：