高校数学の「軸が移動する放物線の最大値」に関する問題を解いてみる。【Yahoo!知恵袋より】

2022年7月3日2023年1月8日二次関数大学入学共通テスト,大学入試センター試験,実用数学技能検定（数学検定 数検),数検2級,数検準2級

Yahoo!知恵袋の高校数学カテゴリに掲載されていた「軸が移動する放物線の最大値」に関する問題を解いてみました。

解法

\( \ y=x^2+ax+b \ \) を変形して、軸と頂点を求める。
\( \ y=\left( x+\displaystyle\frac{1}{2}a\right)^2-\displaystyle\frac{a^2}{4}+b \ \)
軸は\( \ x=-\displaystyle\frac{a}{2} \ \) , 頂点の座標は \( \ \left( -\displaystyle\frac{a}{2} \ , \ -\displaystyle\frac{a^2}{4}+b\right) \ \)

以下、軸と定義域との位置関係をもとに最大値を求めていく。

定義域が0以上3以下のとき

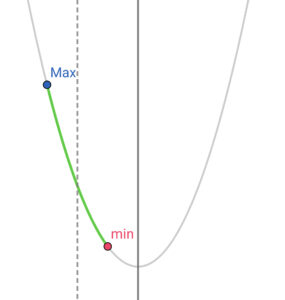	1) \( \ 3 \lt -\displaystyle\frac{1}{2}a \ \) すなわち、\( \ -6 \gt a \ \)のとき、 最大値は\( \ f\left( 0\right)=b=1 \ \)
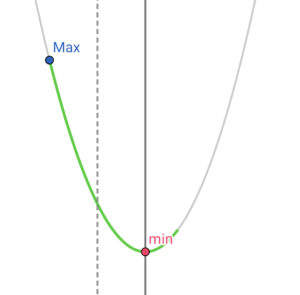	2) \( \ \displaystyle\frac{3}{2} \lt -\displaystyle\frac{1}{2}a \lt 3 \ \) すなわち、\( \ -6 \lt a \lt -3 \ \) のとき、 最大値は\( \ f\left( 0\right)=b=1 \ \)
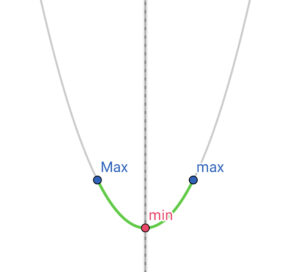	3) \( \ \displaystyle\frac{3}{2}=-\displaystyle\frac{1}{2}a \ \) すなわち \( \ a=-3 \ \) のとき、 最大値は \( \ f\left( 0\right)=b=1 \ \)
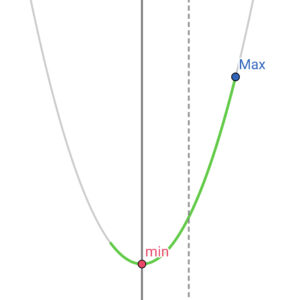	4) \( \ 0 \lt -\displaystyle\frac{1}{2}a \lt \displaystyle\frac{3}{2} \ \) すなわち、\( \ -3 \lt a \lt 0 \ \)のとき、 最大値は\( \ f\left( 3\right)=3a+b=-8 \ \)
	5) \( \ -\displaystyle\frac{1}{2}a \lt 0 \ \) すなわち、\( \ a \gt 0 \ \) のとき、 最大値は、\( \ f\left( 3\right)=3a+b=-8 \ \)

定義域が0以上6以下のとき

	1) \( \ 6 \lt -\displaystyle\frac{1}{2}a \ \) すなわち、\( \ -12 \gt a \ \)のとき、 最大値は\( \ f\left( 0\right)=b=9 \ \)
	2) \( \ 3 \lt -\displaystyle\frac{1}{2}a \lt 6 \ \) すなわち、\( \ -12 \lt a \lt -6 \ \) のとき、 最大値は\( \ f\left( 0\right)=b=9 \ \)
	3) \( \ 3=-\displaystyle\frac{1}{2}a \ \) すなわち \( \ a=-6 \ \) のとき、 最大値は \( \ f\left( 0\right)=b=9 \ \)
	4) \( \ 0 \lt -\displaystyle\frac{1}{2}a \lt 3 \ \) すなわち、\( \ -6 \lt a \lt 0 \ \)のとき、 最大値は\( \ f\left( 6\right)=6a+b=-27 \ \)
	5) \( \ -\displaystyle\frac{1}{2}a \lt 0 \ \) すなわち、\( \ a \gt 0 \ \) のとき、 最大値は、\( \ f\left( 6\right)=6a+b=-27 \ \)

まとめると
\( \ 3 \lt a \ \) のとき、 \( \ \begin{eqnarray} \left\{ \begin{array}{l} 3a + b = -8 \\ 6a + b = 27 \end{array} \right. \end{eqnarray} \ \)

この連立方程式を解いて、 \( \ \begin{eqnarray} \left\{ \begin{array}{l} a=-\displaystyle\frac{19}{3} \\ b = 11 \end{array} \right. \end{eqnarray} \ \)

こたえ

\( \ \begin{eqnarray} \left\{ \begin{array}{l} a=-\displaystyle\frac{19}{3} \\ b = 11 \end{array} \right. \end{eqnarray} \ \)

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：