列車トンネル問題
中学数学で、難問の部類に入るのが、
「列車と橋（またはトンネル）」の問題です。
しかし、本当に難しいのでしょうか。
この問題が一見難しく思えるのは、日常生活との「視点」の違いがあるからです。
公共交通機関は、老若男女問わず利用することができますが、
その乗り物の中で、中学生では立ち入れない場所がありますよね。「そこ」を意識することがポイントなんです。
[mathjax]
列車の長さを\(y\) mとします。
この問題を解く「私たち」は「どこ」にいるのか。
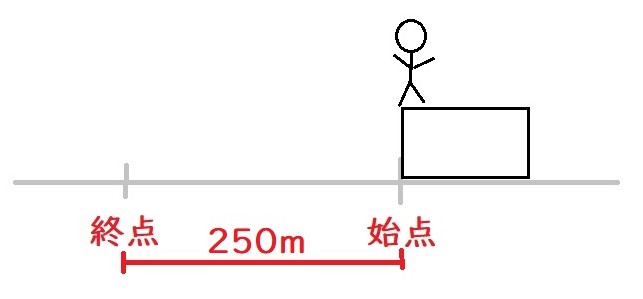
「渡り終わる」、「渡りきる」があったら、列車の最後尾を意識する。
私たちは運転席にいるわけですから、250mの鉄橋も、列車に乗っている誰よりも早く渡り始めます。
ということは当然、行く手に見える「鉄橋の終点」にも、一番のりしますね。
しかし、問題には「渡り終わるまで」とありますから、
運転席の私たちは、列車の最後尾にいる車掌さんが鉄橋の終点に到達するまで、つまり列車の長さぶんだけ、走らねばなりません。
- つまり、運転手は、\(250+y\) mの距離を25秒で走った。ということになりますね。
測り始めたのは、「いつ」？
次は、トンネルの方の問題です。
トンネルに列車全体が隠れていた時間を測るためのストップウォッチのスタートボタンは、いったいいつ押したのでしょう。
運転手がトンネルに入った瞬間？
いやいや、列車は見えていますから、隠れたことになりませんね。
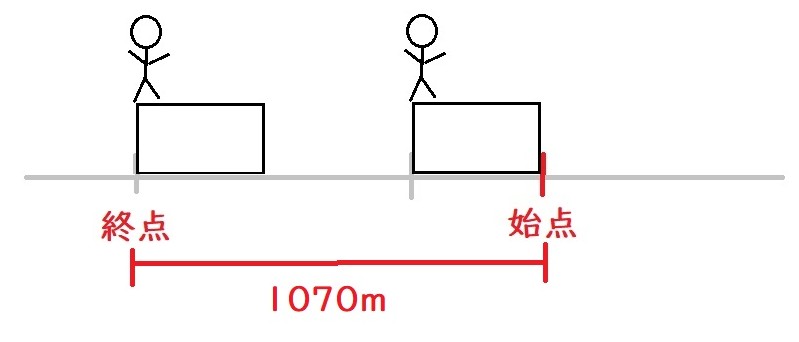
今回は、車掌さんがいる列車の最後尾がトンネルの始点と重なったときに、ボタンを押したのです。
目線が変わったの？
こういう問題は、運転手目線で。と言ったのに、
早々にその考えを変えなくてはならないのか。というと、
そんなことはありません。
車掌さんのいる列車の最後尾とトンネルの始点が重なったとき、
運転席の私達は、トンネルの中を、列車の長さぶん移動しています。
つまり、全長1070mのトンネルの \(y\) m地点で、
ストップウォッチが押され、計測が始まったのです。
\( 1070-y\) mを35秒で移動したことになります。
ゆえに、この列車の秒速を \(\LARGE x=\frac{1070-y}{35}\) と表すことができます。
2つの式を計算します。
\(\LARGE \frac{250+y}{25} = \frac{1070-y}{35}\)を解いて、
こうして、\( x=22\) が求まります。
列車の長さは、300mとわかりました。
電車ゲームのつもりで数学を解こう！
どんな教科でもそうですが、自分がどこにいるのか。という視点を定めることで、問題が解きやすくなることが多いです。
自分が運転しているような感覚が楽しめる電車ゲームがありますが、それをやっているようなつもりで数学を解いてみましょう。
共有:
プロフィール
