平面ベクトル三角形の内分比を統一する（その4）【たすきがけで比を統一せよ!!】

図に内分比を書き込んで楽に解く。

Lukia

この内分比からあるベクトルを表現するという問題は、ベクトルを習ったばかりの定期テストならば、高配点の問題かもしれませんが、
入試問題では、かなり序盤の小問にすぎません。
よって、紙面をこういう問題に割く余裕もないので、できれば図（適当でOK）を描いて、内分比を書き込み、比を統一して一気に解いてしまいましょう。

Lukia

適当な三角形\( \ \mathrm{OAB} \ \)を描き,
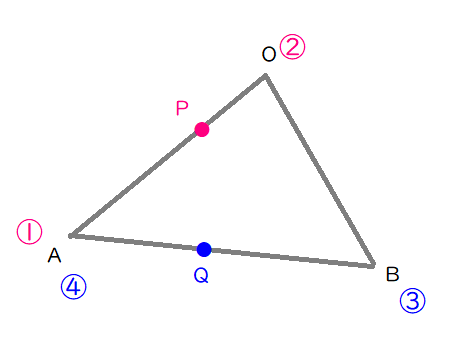
内分点を打ち、内分比を互い違いの頂点に書き留めておきます。
点\( \ \mathrm{P} \ \)は 辺\( \ \mathrm{OA} \ \)を\( \ 1:2 \ \)に内分する.とあるので、
内分点自体は\( \ \mathrm{OP}:\mathrm{PA}=1:2 \ \)となるように打つのですが、
内分比は、頂点\( \ \mathrm{O} \ \)のほうに\( \ \color{#f700ca}{②} \ \)を書き、
頂点\( \ \mathrm{A} \ \)のほうに\( \ \color{#f700ca}{①} \ \)を書いています。

Lukia

辺\( \ \mathrm{AB} \ \)についても同様の操作を行っています。

Lukia

よく見ると、頂点\( \ \mathrm{A} \ \)には\( \ \color{#f700ca}{①} \ \)と\( \ \color{#0004fc}{④} \ \)というふたつの内分比がおかれていますね。
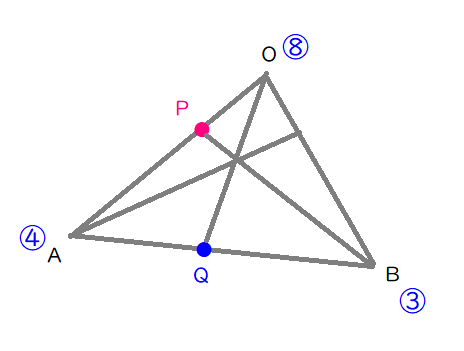
ここで、ピンク色で示された内分比を4倍して、青色で示された内分比に統一していまいます。

Lukia

さらに、内分点と、対頂角を結んで、線分を描き込んでおきましょう。
線分\( \ \mathrm{OQ} \ \)と線分\( \ \mathrm{BP} \ \)の交点と頂点\( \ \mathrm{A} \ \)を通る線分も引いておきます。
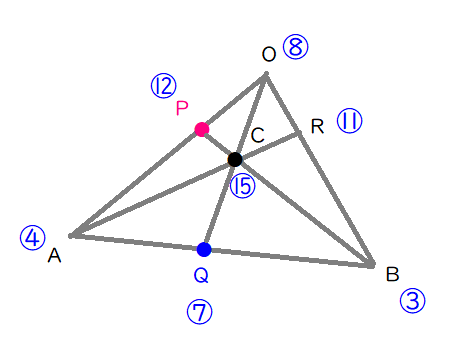
これより、辺\( \ \mathrm{OB} \ \)を\( \ 3:8 \ \)に内分する点を\( \ \mathrm{R} \ \)とおくことにし、
さらに3つの線分の交点を\( \ \mathrm{C} \ \)とします。

Lukia

ふたつの頂点に書かれた内分比の和を内分点に書いていきます。
内分点\( \ \mathrm{P} \ \)：\( \ 4+8=12 \ \)
内分点\( \ \mathrm{Q} \ \)：\( \ 4+3=7 \ \)
内分点\( \ \mathrm{R} \ \)：\( \ 3+8=11 \ \)
さらに、点\( \ \mathrm{C} \ \)は、線分\( \ \mathrm{AS} \ \)または線分\( \ \mathrm{BP} \ \)または線分\( \ \mathrm{OQ} \ \)の内分点だといえますね。
内分点\( \ \mathrm{C} \ \)：\( \ 4+11=3+12=8+7=15 \ \) とわかります。

Lukia

あとは、頂点または内分点に書かれた比を拾いながら、ベクトルの形で表現していくだけになります。
\( \ 15\overrightarrow{\mathrm{OC}}=4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}} \ \)
両辺を\( \ 15 \ \)で割って、
\( \ \overrightarrow{\mathrm{OC}}=\displaystyle\frac{1}{15}\left( 4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right) \ \)

Lukia

手順を少していねいに書いたので、記事としては長くなってしまいましたが、実際には以下の図を描いてしまえば、一気に答えが求められることになりますね。

$$\overrightarrow{\mathrm{OC}}=\displaystyle\frac{1}{15}\left( 4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right) $$

定期テストならこっちで解くべきかも。

Lukia

ベクトルを習ったばかりの定期テストならば、上記のような「図で内分比をわりだしておいて、こたえだけを書く。」なんて解法は減点対象となってしまうかもしれませんので、
一応、定期テスト用の解法も示しておきたいと思います。

$$\begin{align}条件より,&\overrightarrow{\mathrm{OP}}=\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OA}} \\\\ &\overrightarrow{\mathrm{OQ}}=\displaystyle\frac{1}{7}\left( 4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right)\quad である.\end{align}$$
$$\begin{align}点\mathrm{C}は&線分\mathrm{BP}を\quad s:1-s\quad\left( 0 \lt s \lt 1\right) に内分するので, \\\\ &\overrightarrow{\mathrm{OC}}=s\overrightarrow{\mathrm{OP}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}}\quad \cdots\cdots \ ① \\\\ また,点\mathrm{C}は&線分\mathrm{OQ}上にあるので,\\\\ &\overrightarrow{\mathrm{OC}}=k\overrightarrow{\mathrm{OQ}}\quad \left( k \ は実数\right) \quad \cdots\cdots \ ② \end{align}$$
$$\begin{align}①=②\quad より& \\\\ &\displaystyle\frac{k}{7}\left( 4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right)=\displaystyle\frac{s}{3}\overrightarrow{\mathrm{OA}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}} \\\\ &\displaystyle\frac{4}{7}k=\displaystyle\frac{s}{3}\quad より\quad s=\displaystyle\frac{12}{7}k\\\\ &\displaystyle\frac{3}{7}k=1-s\\\\ &3k=7-12k\quad より\\\\ &k=\displaystyle\frac{7}{15}\\\\ \\\\ ゆえに,\quad &\overrightarrow{\mathrm{OC}}=\displaystyle\frac{1}{15}\left( 4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right) \end{align}$$

Lukia

どうです、めんどくさいでしょ？（笑）
ふたつの実数\( \ k \ \)や\( \ s \ \)をおき、
さらにそれぞれがどんな数かことわりも入れねばならず、
最終的には連立方程式を解いていかねばならないので、チョ～時間がかかるのです。

Lukia

定期テストは、「習ったことが習った通りに再現できるか。」を確認するために行われているようなものだと思いますので、はしょったやり方は通用しないと考えておいたほうがよいでしょう。
しかし、大学入試では、かなり序盤の小問扱いとなる可能性が大きいです。
どんどん解き進めるには、こんなに時間（や行数）はかけられないので、下書き用紙などにさっさと図を描いて、解いてしまいましょう。

こたえ

$$\overrightarrow{\mathrm{OC}}=\displaystyle\frac{1}{15}\left( 4\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right) $$