平面ベクトル三角形の内分比を統一する（その3）【たすきがけで比を統一せよ!!】

2023年1月8日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

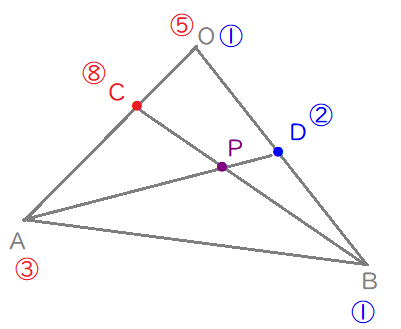
(1) 図を描いて、内分比を「統一」する。

Lukia

まずは、図を描いて、わかっている情報を書き込みます。
すると、赤で示した内分比と、青で示した内分比は統一できそうですね。
しかも、今回は、青を5倍するだけなので、楽ができそうです。

Lukia

内分比を統一したことで、点\(\mathrm{P}\)の比も\(13\)とわかりました。

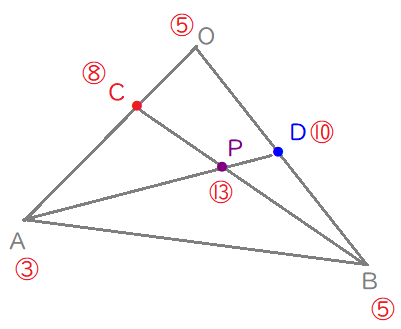
$$\begin{align}点\mathrm{P}は線分&\mathrm{AD}を \ 10:3 \ に内分するから,\\\\ \mathrm{AP:PD}=&\displaystyle\frac{10}{13}:\displaystyle\frac{3}{13}\\\\ \\\\ゆえに\quad s=&\displaystyle\frac{10}{13}\end{align}$$
$$\begin{align}点\mathrm{P}は線分&\mathrm{BC}を \ 8:5 \ に内分するから,\\\\ \mathrm{BP:PC}=&\displaystyle\frac{8}{13}:\displaystyle\frac{5}{13}\\\\ \\\\ゆえに\quad t=&\displaystyle\frac{8}{13}\end{align}$$

$$s=\displaystyle\frac{10}{13} \ , \ t=\displaystyle\frac{8}{13}$$

(2) を解く。

Lukia

問題の指示通りに、線分\(\mathrm{OQ}\)を示します。
これによって、点\(\mathrm{P}\)が線分\(\mathrm{OQ}\)を\(8:5\)に内分することがわかりました。

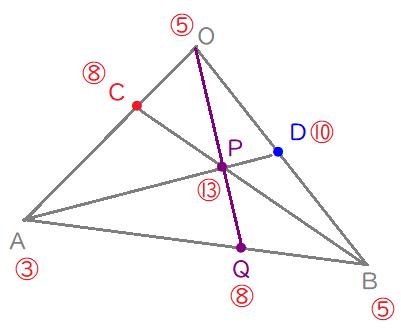
$$\begin{align}\overrightarrow{\mathrm{OP}}=&\displaystyle\frac{8}{13}\overrightarrow{\mathrm{OQ}} \ より, \\\\ \overrightarrow{\mathrm{OQ}}=&\displaystyle\frac{13}{8}\overrightarrow{\mathrm{OP}}\end{align}$$

こたえ

$$\begin{align}\left( 1\right)\quad& s=\displaystyle\frac{10}{13} \ , \ t=\displaystyle\frac{8}{13} \\\\ \\\\\left( 2\right) \quad& \overrightarrow{\mathrm{OQ}}=\displaystyle\frac{13}{8}\overrightarrow{\mathrm{OP}}\end{align}$$

平面ベクトル三角形の内分点 記事一覧【たすきがけで比を統一せよ!!】

平面ベクトルの習い始めによく演習する「三角形の内分点」に関する問題を集めました。一見難しそうな外 ...

 https://makelemonadejp.com/plane-vector-internal-division-of...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。