平面ベクトル 三角形の内分比を統一する(その1)【たすきがけで比を統一せよ!!】

線分\(\mathrm{CD}\)と線分\(\mathrm{BE}\)との交点を\(\mathrm{P}\)とするとき、\(\overrightarrow{\mathrm{AP}}\)を\(\overrightarrow{\mathrm{AB}}\)と\(\overrightarrow{\mathrm{AC}}\)を用いて表せ。

Lukia
ベクトルを勉強した直後の定期テストでは使えないかもしれませんが、あとに難しい問題がひかえているようなセンター試験や数学検定などには使えると思います。
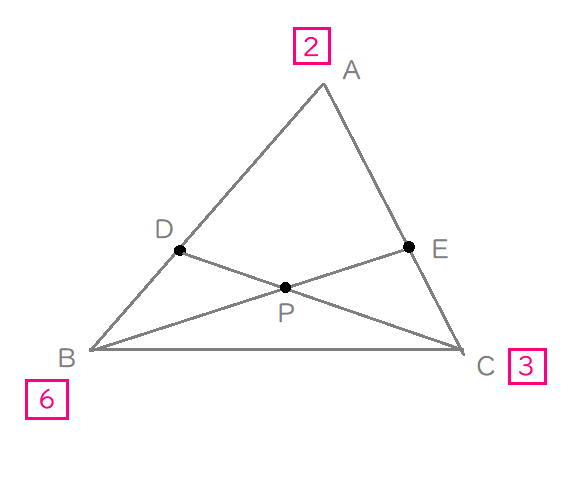
内分点Dを打って、頂点に比を書き込む。

Lukia

れもん
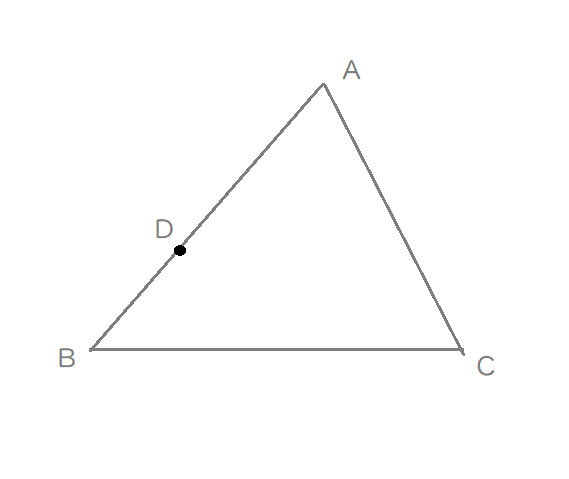

Lukia
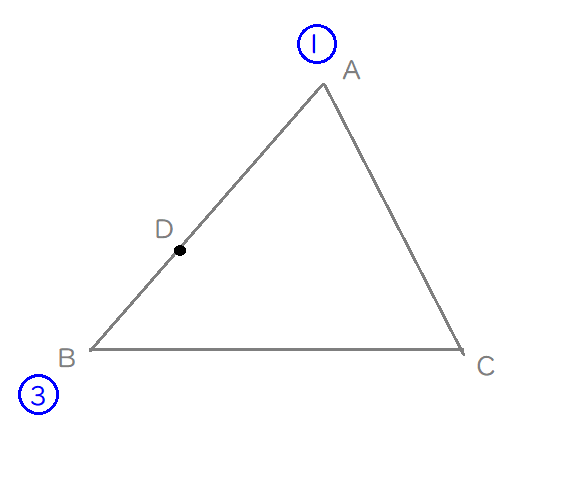

れもん
ちなみに、比の値に青いまるがしてあるのは、なにか理由があるんですか?

Lukia
では、同様に、辺\(\mathrm{AC}\)を\(3:2\)に内分する点\(\mathrm{E}\)を打ってみましょう。
れもんさん、お願いできますか?

れもん
まず、\(\mathrm{AE}:\mathrm{EC}=3:2\)となるように点\(\mathrm{E}\)を打って・・・
内分比をたすきがけして、頂点に比を書き込む・・・っと。
こんな感じですか?
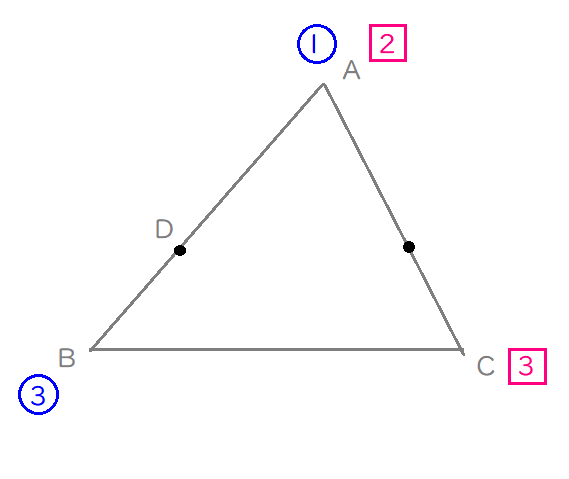

Lukia
こうしてみると、点\(\mathrm{A}\)にある比は、\(\color{#0004fc}{1}\)と\(\color{#f700ca}{2}\)の2通りで示されていることになりますね。
統一したいのですが、どうすればいいですか?

れもん

Lukia
ですから、改めて書き直すとこうなりますね。
このように、ひとつの頂点に異なる比が割り当てられたとき、その最小公倍数を書き込めばすべての比を統一できます。
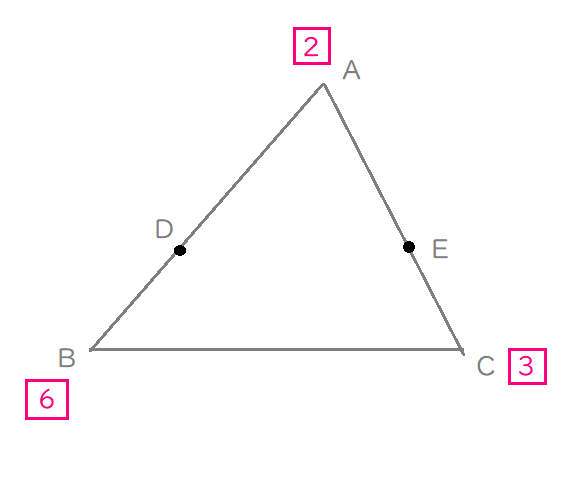
内分点に「内分比の和」を割り当てる。

Lukia

Lukia
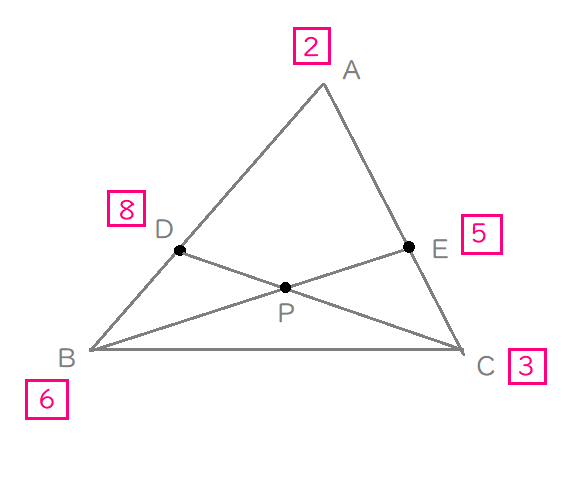
だから、点\(\mathrm{D}\)は、\(2+6=8\)を書き込み、
点\(\mathrm{E}\)は、\(2+3=5\)を書き込みます。

れもん

Lukia
線分\(\mathrm{BE}\)に着目すれば、点\(\mathrm{P}\)は・・・?

れもん

Lukia
では、線分\(\mathrm{CD}\)に着目すれば、点\(\mathrm{P}\)は・・・?

れもん

Lukia

れもん
表現しよう。

Lukia
今回、\(\overrightarrow{\mathrm{AP}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}}\)
(ただし、\(s \ , \ t \)は実数)
という形で表現せよ。ということですね。
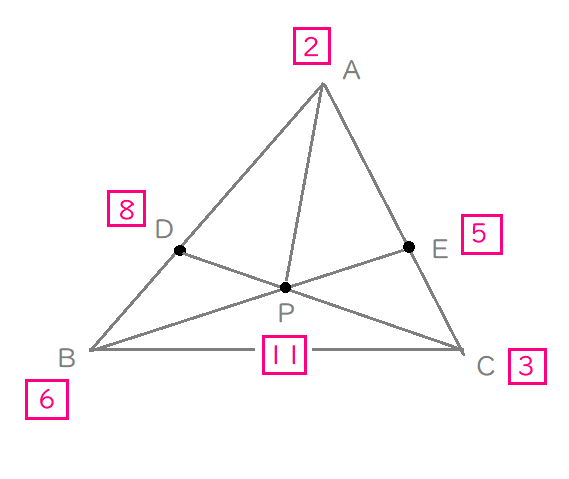
点\(A\)は起点となっているので、無視して、それ以外の\(\mathrm{B \ , \ C \ , \ P}\)にそれぞれ比の値をつけて表現すれば、ほぼ完成です。

れもん
\(\Large 11\overrightarrow{\mathrm{AP}}=6\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}}\) ですか?

Lukia

れもん
\(\Large \overrightarrow{\mathrm{AP}}=\displaystyle\frac{6}{11}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{3}{11}\overrightarrow{\mathrm{AC}}\) ですね。

Lukia
このように、手順を覚えてしまえば、機械的に解くことができます。
ちなみに。

Lukia
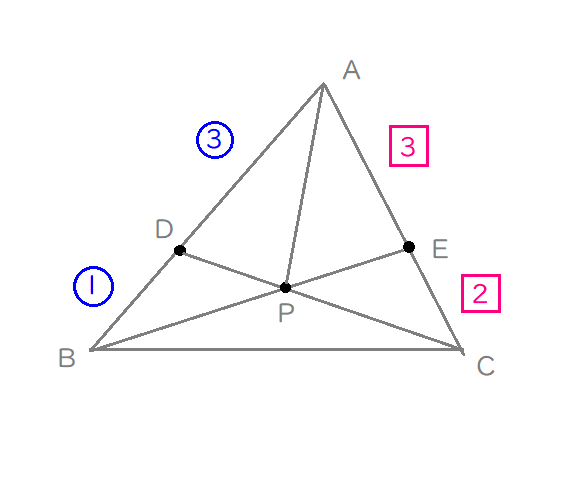
$$\begin{align}ⅰ)\quad \triangle \mathrm{ADC} \ について \\\\ \overrightarrow{\mathrm{AP}}=&s\overrightarrow{\mathrm{AD}}+\left( 1-s\right)\overrightarrow{\mathrm{AC}} \ \left( 0 \leqq s \leqq 1\right)
\\\\ =&\displaystyle\frac{3}{4}s\overrightarrow{\mathrm{AB}}+\left( 1-s\right)\overrightarrow{\mathrm{AC}} \cdots①\end{align}$$
$$\begin{align}ⅱ)\quad \triangle \mathrm{ABE} \ について \\\\ \overrightarrow{\mathrm{AP}}=&t\overrightarrow{\mathrm{AB}}+\left( 1-t\right)\overrightarrow{\mathrm{AC}} \ \left( 0 \leqq t \leqq 1\right)
\\\\ =&t\overrightarrow{\mathrm{AB}}+\left( 1-t\right)\cdot \displaystyle\frac{3}{5}\overrightarrow{\mathrm{AC}} \cdots②\end{align}$$
① , ②より、
$$\begin{align}\displaystyle\frac{3}{4}s\overrightarrow{\mathrm{AB}}+\left( 1-s\right)\overrightarrow{\mathrm{AC}}=&t\overrightarrow{\mathrm{AB}}+\left( 1-t\right)\cdot \displaystyle\frac{3}{5}\overrightarrow{\mathrm{AC}} \\\\ \\\\ \\\\ \displaystyle\frac{3}{4}s=&t\cdots③\\\\ \left( 1-s\right)=&\left( 1-t\right)\cdot \displaystyle\frac{3}{5}\cdots④ \end{align}$$
$$\begin{align}5\left( 1-s\right)=&3\left( 1-\displaystyle\frac{3}{4}s\right) \\\\ 5-5s=&3-\displaystyle\frac{9}{4}s \\\\ 2=&\displaystyle\frac{11}{4}s\\\\ s=&\displaystyle\frac{8}{11} \end{align}$$
これを①に代入して、
$$\begin{align}\overrightarrow{\mathrm{AP}}=&\displaystyle\frac{3}{4}\cdot \displaystyle\frac{8}{11}\overrightarrow{\mathrm{AB}}+\left( \displaystyle\frac{11-8}{11}\right)\overrightarrow{\mathrm{AC}} \\\\ \overrightarrow{\mathrm{AP}}=&\displaystyle\frac{6}{11}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{3}{11}\overrightarrow{\mathrm{AC}} \end{align}$$
こたえ
$$\Large \overrightarrow{\mathrm{AP}}=\displaystyle\frac{6}{11}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{3}{11}\overrightarrow{\mathrm{AC}}$$
 以下の記事一覧に他のボリュームのブログカードを載せています。
以下の記事一覧に他のボリュームのブログカードを載せています。途中のボリュームからお読みになった方はこちらからどうぞ。
[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません