【 08 / 12 】高校数学の「平面ベクトルの点Pの存在範囲」に関する問題を解いてみる。

読了時間: 約4分38秒
[mathjax]問題
\( \ \triangle \mathrm{OAB} \ \)について点\( \ \mathrm{P} \ \)が
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
と \( \ \vert s+t \vert \leq 2 \ , \ st \geq 0 \ \)を満たしながら動くとき、
点\( \ \mathrm{P} \ \)の存在範囲を示せ。
( ただし\( \ s \ \) , \( \ t \ \) はともに実数とする )
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
と \( \ \vert s+t \vert \leq 2 \ , \ st \geq 0 \ \)を満たしながら動くとき、
点\( \ \mathrm{P} \ \)の存在範囲を示せ。
( ただし\( \ s \ \) , \( \ t \ \) はともに実数とする )
解法
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
\( \ \vert s+t \vert \leq 2 \ , \ st \geq 0 \ \)
$$\begin{align}&\vert s+t \vert \leq 2 \\\\-2 \leq &s+t \leq 2\end{align}$$
\( \ -2 \leq s+t \leq 2 \ \)の各辺を\( \ 2 \ \)で割って
$$-1 \leq \frac{1}{2}s+\frac{1}{2}t \leq 1$$
また
$$\begin{align}st& \geq 0 \\\\ s& \geq 0 \ かつ \ t \geq 0 \\\\ または&\\\\ s& \lt 0 \ かつ \ t \lt 0 \end{align}$$
以上より
$$\begin{align}-1 \leq &\frac{1}{2}s+\frac{1}{2}t \leq 1 \ , \ s \geq 0 \ かつ \ t \geq 0 \\\\ または& \\\\ -1 \leq &\frac{1}{2}s+\frac{1}{2}t \leq 1 \ , \ s \lt 0 \ かつ \ t \lt 0 \end{align}$$
ここで、\(\Large \frac{1}{2}\)\( \ s=k \ \) とし、
\(\Large \frac{1}{2}\)\( \ t=l \ \) とする。
$$\begin{align}\overrightarrow{\mathrm{OP}}=&2\cdot \frac{1}{2}s\overrightarrow{\mathrm{OA}}+2\cdot \frac{1}{2}t\overrightarrow{\mathrm{OB}} \\\\ =&2k\overrightarrow{\mathrm{OA}}+2l\overrightarrow{\mathrm{OB}}\\\\ \\\\ ここで、& \ 2\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA’}} \\\\ & \ 2\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB’}} \quad とすると、\\\\ \\\\ \overrightarrow{\mathrm{OP}}=&k\overrightarrow{\mathrm{OA’}}+l\overrightarrow{\mathrm{OB’}} \\\\ &-1 \leq k+l \leq 1 \ , \ kl \geq 0 \end{align}$$

ゆえに点\( \ \mathrm{P} \ \)は三角形\( \ \mathrm{OA’B’} \ \) の周上とその内部、
または三角形\( \ \mathrm{OA"B"} \ \) の周上とその内部に存在する。
\( \ \vert s+t \vert \leq 2 \ , \ st \geq 0 \ \)
$$\begin{align}&\vert s+t \vert \leq 2 \\\\-2 \leq &s+t \leq 2\end{align}$$
\( \ -2 \leq s+t \leq 2 \ \)の各辺を\( \ 2 \ \)で割って
$$-1 \leq \frac{1}{2}s+\frac{1}{2}t \leq 1$$
また
$$\begin{align}st& \geq 0 \\\\ s& \geq 0 \ かつ \ t \geq 0 \\\\ または&\\\\ s& \lt 0 \ かつ \ t \lt 0 \end{align}$$
以上より
$$\begin{align}-1 \leq &\frac{1}{2}s+\frac{1}{2}t \leq 1 \ , \ s \geq 0 \ かつ \ t \geq 0 \\\\ または& \\\\ -1 \leq &\frac{1}{2}s+\frac{1}{2}t \leq 1 \ , \ s \lt 0 \ かつ \ t \lt 0 \end{align}$$
ここで、\(\Large \frac{1}{2}\)\( \ s=k \ \) とし、
\(\Large \frac{1}{2}\)\( \ t=l \ \) とする。
$$\begin{align}\overrightarrow{\mathrm{OP}}=&2\cdot \frac{1}{2}s\overrightarrow{\mathrm{OA}}+2\cdot \frac{1}{2}t\overrightarrow{\mathrm{OB}} \\\\ =&2k\overrightarrow{\mathrm{OA}}+2l\overrightarrow{\mathrm{OB}}\\\\ \\\\ ここで、& \ 2\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA’}} \\\\ & \ 2\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB’}} \quad とすると、\\\\ \\\\ \overrightarrow{\mathrm{OP}}=&k\overrightarrow{\mathrm{OA’}}+l\overrightarrow{\mathrm{OB’}} \\\\ &-1 \leq k+l \leq 1 \ , \ kl \geq 0 \end{align}$$
ゆえに点\( \ \mathrm{P} \ \)は三角形\( \ \mathrm{OA’B’} \ \) の周上とその内部、
または三角形\( \ \mathrm{OA"B"} \ \) の周上とその内部に存在する。
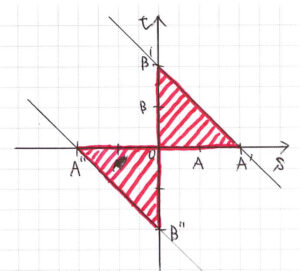
st平面上で考えてみる
\( \ \triangle \mathrm{OAB} \ \)が\( \ xy \ \)平面上ならぬ\( \ st \ \)平面上にあると考えると、
グラフを描けば上のような式の変形をする必要がないかもしれません。
\( \ \vert \overrightarrow{\mathrm{OA}} \vert=1 \ \) (\( \ s=1 \ \))、
\( \ \vert \overrightarrow{\mathrm{OB}} \vert=1 \ \) (\( \ t=1 \ \))とします。
\( \ st \ \)平面上に\( \ t=2-s \ \)と\( \ t=-2-s \ \)のグラフを描きます。
点\( \ \mathrm{A’} \ \)は、\( \ \left( s \ , \ t\right)=\left( 2 \ , \ 0\right) \ \) に、
点\( \ \mathrm{B’} \ \)は、\( \ \left( s \ , \ t\right)=\left( 0 \ , \ 2\right) \ \)に、
点\( \ \mathrm{A"} \ \)は、\( \ \left( s \ , \ t\right)=\left( -2 \ , \ 0\right) \ \) に、
点\( \ \mathrm{B"} \ \)は、\( \ \left( s \ , \ t\right)=\left( 0 \ , \ -2\right) \ \)に置かれるとわかります。
以下の4つの条件を満たす領域を求めます。
$$\begin{align}t \leq &2-s \\\\ t \geq &-2-s \\\\ 線分&\mathrm{A’A"}\\\\ 線分&\mathrm{B’B"} \end{align}$$

求める領域は、\( \ \triangle \mathrm{OA’B’} \ \)の周上とその内部、または\( \ \triangle \mathrm{OA"B"} \ \)の周上とその内部とわかります。
よって、こたえは「 三角形\( \ \mathrm{OA’B’} \ \) の周上とその内部、 または三角形\( \ \mathrm{OA"B"} \ \) の周上とその内部に存在する。 」となります。
グラフを描けば上のような式の変形をする必要がないかもしれません。
\( \ \vert \overrightarrow{\mathrm{OA}} \vert=1 \ \) (\( \ s=1 \ \))、
\( \ \vert \overrightarrow{\mathrm{OB}} \vert=1 \ \) (\( \ t=1 \ \))とします。
\( \ st \ \)平面上に\( \ t=2-s \ \)と\( \ t=-2-s \ \)のグラフを描きます。
点\( \ \mathrm{A’} \ \)は、\( \ \left( s \ , \ t\right)=\left( 2 \ , \ 0\right) \ \) に、
点\( \ \mathrm{B’} \ \)は、\( \ \left( s \ , \ t\right)=\left( 0 \ , \ 2\right) \ \)に、
点\( \ \mathrm{A"} \ \)は、\( \ \left( s \ , \ t\right)=\left( -2 \ , \ 0\right) \ \) に、
点\( \ \mathrm{B"} \ \)は、\( \ \left( s \ , \ t\right)=\left( 0 \ , \ -2\right) \ \)に置かれるとわかります。
以下の4つの条件を満たす領域を求めます。
$$\begin{align}t \leq &2-s \\\\ t \geq &-2-s \\\\ 線分&\mathrm{A’A"}\\\\ 線分&\mathrm{B’B"} \end{align}$$

求める領域は、\( \ \triangle \mathrm{OA’B’} \ \)の周上とその内部、または\( \ \triangle \mathrm{OA"B"} \ \)の周上とその内部とわかります。
よって、こたえは「 三角形\( \ \mathrm{OA’B’} \ \) の周上とその内部、 または三角形\( \ \mathrm{OA"B"} \ \) の周上とその内部に存在する。 」となります。

ベクトルと考えるから難しいのであって、 \( \ s \ \)と\( \ t \ \)に関する領域の問題。と考えればよいのではないかな。と思っています。
式変形はできたほうがいいに決まっていますが、この領域の問題。という考え方を確かめる術にしながら、式変形の練習をしていくのが習得の近道になるかも。
式変形はできたほうがいいに決まっていますが、この領域の問題。という考え方を確かめる術にしながら、式変形の練習をしていくのが習得の近道になるかも。
こたえ
三角形\( \ \mathrm{OA’B’} \ \) の周上とその内部、 または三角形\( \ \mathrm{OA"B"} \ \) の周上とその内部に存在する。


[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません