中学数学の2種類の濃度の食塩水を混ぜる問題(その8)

読了時間: 約7分24秒
[mathjax]

Lukia
いよいよ2種類の濃度の食塩水を混ぜる問題も、ラスト2つとなりました。
今回と、次回は、少し難しい部類に入ると思います。
「表を描いて、ていねいに数字をあてはめていく」という作業がどのぐらい役に立つのか。というのを確かめてみるだけでも、十分意味がありますからね。
今回と、次回は、少し難しい部類に入ると思います。
「表を描いて、ていねいに数字をあてはめていく」という作業がどのぐらい役に立つのか。というのを確かめてみるだけでも、十分意味がありますからね。

Lukia
それでは、さっそく下に問題を示します。
少しの間、スクロールの手を止めて解いてみてください。
少しの間、スクロールの手を止めて解いてみてください。
問題
容器Aには6%の食塩水が、容器Bにはある濃度の食塩水が、それぞれ400gずつ入っている。
容器Aから何gか取り出して容器Bに入れ、よくかき混ぜると14%の食塩水になった。
次に、容器Aから取り出したのと同じ重さだけ容器Bから取り出して容器Aに戻したところ、
容器Aの食塩水の濃度は9%になった。
はじめに容器Aから取り出した食塩水の重さは何gか。
容器Aから何gか取り出して容器Bに入れ、よくかき混ぜると14%の食塩水になった。
次に、容器Aから取り出したのと同じ重さだけ容器Bから取り出して容器Aに戻したところ、
容器Aの食塩水の濃度は9%になった。
はじめに容器Aから取り出した食塩水の重さは何gか。
細かく分ける。

もも
う~わっ、数学なのに、問題文が長いですねぇ。

Lukia
そうですねぇ。食塩水の問題を解き始めたころだったら、「見なかったことにしよう・・・」と思ってしまいそうですが、よくよく見てみると、これまでに扱った問題と似ているところがありますよね。

もも
ひとまず、問題文を小分けにしてみようかな。
読んでいくと、混ぜ合わせるという操作を2回やっていますよね。
ということは、前半は「次に」の前までで、
「次に」以降は後半。としてよさそうですね。
読んでいくと、混ぜ合わせるという操作を2回やっていますよね。
ということは、前半は「次に」の前までで、
「次に」以降は後半。としてよさそうですね。

Lukia
いいですねぇ。
人間って、いっぺんにいろんなことをするという「マルチタスク」に向いてないので、
タスクを細かく分けることは大切なんですよね。
人間って、いっぺんにいろんなことをするという「マルチタスク」に向いてないので、
タスクを細かく分けることは大切なんですよね。
前半(「次に」の前まで)
問題
容器Aには6%の食塩水が、容器Bにはある濃度の食塩水が、それぞれ400gずつ入っている。
容器Aから何gか取り出して容器Bに入れ、よくかき混ぜると14%の食塩水になった。
容器Aから何gか取り出して容器Bに入れ、よくかき混ぜると14%の食塩水になった。
表に書き込む。

もも
じゃ、まずは、いつものように、横長の線を3本と、それを4等分するように縦の線を3本引きます。

Lukia
以下のような表になりますね。
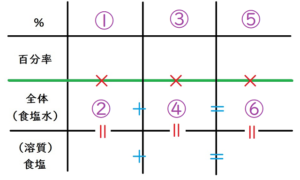

もも
はい。
そして、①から⑥の中で、数字が書き込めそうなところを探して書き込みます。
今回は、縦の列で、左から2番目が容器Aの食塩水、
左から3番目が、容器Bの食塩水とします。
すると、①が6、
③は「ある濃度」とあるから、飛ばしておこう。
そして、①から⑥の中で、数字が書き込めそうなところを探して書き込みます。
今回は、縦の列で、左から2番目が容器Aの食塩水、
左から3番目が、容器Bの食塩水とします。
すると、①が6、
③は「ある濃度」とあるから、飛ばしておこう。

もも
途中を読み飛ばして、最後に14%の食塩水になった。とあるから、
⑤が14となりますよね。
⑤が14となりますよね。

もも
②と④と⑥を埋めたいけれど、少し難しいな・・・
AとBは、400gずつ入っているとあるから、
②と④に400を入れられそうだけど・・・
AとBは、400gずつ入っているとあるから、
②と④に400を入れられそうだけど・・・

もも
400gを混ぜ合わせるわけじゃないんだ!

Lukia
はい。
問題文の4行目からを読んでほしいのですが、
「容器Aから何gか取り出す。」とありますね。
はたして、②に400を入れてもよいでしょうか。
問題文の4行目からを読んでほしいのですが、
「容器Aから何gか取り出す。」とありますね。
はたして、②に400を入れてもよいでしょうか。

もも
あ、ホントだ!
容器Aに400gの食塩水が入っているのは、間違いないけど、
400g全部使うわけじゃないんですね。
容器Aに400gの食塩水が入っているのは、間違いないけど、
400g全部使うわけじゃないんですね。

Lukia
そうです。そして、後半の最後の2行を読むと、
求めるのは、「はじめに容器Aから取り出した食塩水の重さ」とありますね。
ではあらためて聞きます。
②には、なんと書き込めばよいでしょうか。
求めるのは、「はじめに容器Aから取り出した食塩水の重さ」とありますね。
ではあらためて聞きます。
②には、なんと書き込めばよいでしょうか。

もも
\(\Large x\) です!

もも
問題文を読むと、容器Aから \(\Large x\) g取り出して、容器Bに入れたとわかるので、
④は、400のままでよさそうですね。
「横はたし算」ルールを適用して、⑥は \(\Large \left( x+400\right)\) とすることができます。
④は、400のままでよさそうですね。
「横はたし算」ルールを適用して、⑥は \(\Large \left( x+400\right)\) とすることができます。

Lukia
そして、容器Bの食塩水の濃度を表す数字が見当たらないので、
③は、\(\Large y\) としておきましょう。
③は、\(\Large y\) としておきましょう。
%を百分率に直しておく。

Lukia
せっかく、前半後半に分けたので、表と式を完成させてしまいましょう。
「似たような作業は一気にやってしまいましょう。」と言いたいところですが、後半に少し難しいところがあるので、
前半を一つの問題。とみなして、一連の作業をこなしてみます。
「似たような作業は一気にやってしまいましょう。」と言いたいところですが、後半に少し難しいところがあるので、
前半を一つの問題。とみなして、一連の作業をこなしてみます。

もも
たまには、Lukia先生の誘導に乗ってみるか♪
百分率に直すのは、簡単。
左から、\(\Large \frac{6}{100}\) ・ \(\Large \frac{y}{100}\) ・ \(\Large \frac{14}{100}\) です。
百分率に直すのは、簡単。
左から、\(\Large \frac{6}{100}\) ・ \(\Large \frac{y}{100}\) ・ \(\Large \frac{14}{100}\) です。
縦はかけ算・横はたし算

Lukia
では、縦はかけ算・横はたし算をして、一気に式を立ててみてください。

もも
は~い。
まず、「縦はかけ算」をしていきます。
左から2番目の列は、\(\Large \frac{6}{100}\times x\) 、
左から3番目の列は、\(\Large \frac{y}{100}\times 400\) 、
右端の列は、\(\Large \frac{14}{100}\times \left( x+400\right)\) となります。
まず、「縦はかけ算」をしていきます。
左から2番目の列は、\(\Large \frac{6}{100}\times x\) 、
左から3番目の列は、\(\Large \frac{y}{100}\times 400\) 、
右端の列は、\(\Large \frac{14}{100}\times \left( x+400\right)\) となります。

もも
さらに、この表の一番下の段の「横はたし算」をすれば、
式は、
\(\Large \frac{6}{100}\times x + \frac{y}{100}\times 400 = \frac{14}{100}\times \left( x+400\right)\)
式は、
\(\Large \frac{6}{100}\times x + \frac{y}{100}\times 400 = \frac{14}{100}\times \left( x+400\right)\)
となります。

もも
あれっ、でも、ひとつの式に2つも文字がある!
計算したくても、計算できない!
計算したくても、計算できない!

Lukia
はい。
式自体は完成しましたから、ひとまずおいといて、
後半に移りましょう。
式自体は完成しましたから、ひとまずおいといて、
後半に移りましょう。
後半(「次に」以降)
問題
次に、容器Aから取り出したのと同じ重さだけ容器Bから取り出して容器Aに戻したところ、
容器Aの食塩水の濃度は9%になった。
はじめに容器Aから取り出した食塩水の重さは何gか。
容器Aの食塩水の濃度は9%になった。
はじめに容器Aから取り出した食塩水の重さは何gか。
表に書き込む。

もも
まずは、「後半」用の表を描いて、数字を埋めていこう。


もも
①は6、
③は \(\Large y\) 、
⑤は・・・9か。
③は \(\Large y\) 、
⑤は・・・9か。

Lukia
ももちゃん、ひっかかったな・・・
( ̄ー ̄)ニヤリッ。
( ̄ー ̄)ニヤリッ。

もも
な、なんですか、その不敵な笑みは。(汗)

Lukia
容器Bは、はたして \(\Large y\) %のままでしょうか。

もも
えっ?

Lukia
今までのことを思い出してみてください。
濃度が異なる2種類の食塩水を混ぜたら、新たな濃度を示す食塩水になっていたんですよ?
濃度が異なる2種類の食塩水を混ぜたら、新たな濃度を示す食塩水になっていたんですよ?

もも
はい・・・。

Lukia
前半では、容器Bに、容器Aからいくらか食塩水を移したんですから、
容器Bは、\(\Large y\) %のままですか?
容器Bは、\(\Large y\) %のままですか?

もも
容器Bは、\(\Large y\) %のまま・・・?
(目は前半部分を泳いでいる)
(目は前半部分を泳いでいる)

もも
じゃない!
14%になってる!!
14%になってる!!

Lukia
そうですね。
実は、前半で立てた式は、容器Bの新しい姿、「ニュー容器B」のことを表しているんですね。
実は、前半で立てた式は、容器Bの新しい姿、「ニュー容器B」のことを表しているんですね。

もも
なんですか、そのだっさいネーミングはッ。

もも
気を取り直して、書き直してみます。
①は6、
③は14、
⑤は9となりますね。
①は6、
③は14、
⑤は9となりますね。

Lukia
はい。
前半で書いておいた \(\Large y\) は使われそうにないですね。
前半で書いておいた \(\Large y\) は使われそうにないですね。

もも
あ、ホントだ。
じゃ、次は、全体の重さの段ですね。
なんだか、操作がややこしいな。
じゃ、次は、全体の重さの段ですね。
なんだか、操作がややこしいな。

Lukia
いま、容器Aの重さは、どうなっていますか?

もも
たしか、もともと400gあったんだけど、
そこから \(\Large x\) g取り出したから・・・
\(\Large \left( 400-x\right)\) かな?
そこから \(\Large x\) g取り出したから・・・
\(\Large \left( 400-x\right)\) かな?

Lukia
そのとおりです。
だから、②には、 \(\Large \left( 400-x\right)\) が入りますね。
だから、②には、 \(\Large \left( 400-x\right)\) が入りますね。

もも
あ、ホントだ。
じゃぁ、容器Bは・・・
じゃぁ、容器Bは・・・

Lukia
ニュー容器Bですよ?

もも
いやですよ~、そのダサい名前は言いたくない~。
あっ、「容器Aから取り出したのと同じ重さだけ取り出した」とあるから、
④は、 \(\Large x\) ですね。
あっ、「容器Aから取り出したのと同じ重さだけ取り出した」とあるから、
④は、 \(\Large x\) ですね。

Lukia
チッ、「ニュー容器B」なのに・・・

もも
ということは、「横はたし算」をすれば、
⑥は、\(\Large \left( 400-x\right)+x=400\) で、
400gとなりますね。
⑥は、\(\Large \left( 400-x\right)+x=400\) で、
400gとなりますね。

Lukia
ふんっ、次に進んでくださいッ!
%を百分率に直しておく。

もも
じゃ、①、③、⑤の%を百分率に直します。
左から、\(\Large \frac{6}{100}\) ・ \(\Large \frac{14}{100}\) ・ \(\Large \frac{9}{100}\) となりますね。
左から、\(\Large \frac{6}{100}\) ・ \(\Large \frac{14}{100}\) ・ \(\Large \frac{9}{100}\) となりますね。
縦はかけ算・横はたし算

もも
ということは、もう「縦はかけ算・横はたし算」で一番下の段のマスをうめていくんだな。
ですよねぇ~、Lukia先生?
ですよねぇ~、Lukia先生?

Lukia
ダサイって言われた・・・(涙)

もも
なんでいじけてんですか。(笑)
ま、いいや。
ま、いいや。

もも
まず、それぞれの縦の列のかけ算をしていきます。
左から、
\(\Large \frac{6}{100}\times \left( 400-x\right)\) 、
\(\Large \frac{14}{100}\times x\) 、
\(\Large \frac{9}{100}\times 400\) となります。
左から、
\(\Large \frac{6}{100}\times \left( 400-x\right)\) 、
\(\Large \frac{14}{100}\times x\) 、
\(\Large \frac{9}{100}\times 400\) となります。
一番下の段の「たし算」をする。

もも
Lukia先生、容器Aと、に、にゅー容器Bの計算を済ませましたよ。

Lukia
(ハッ!)
も、ももちゃん、今「ニュー容器B」って言ってくれました?
も、ももちゃん、今「ニュー容器B」って言ってくれました?

もも
は、はい。言いましたよ。

Lukia
ねっ、ねっ、やっぱり「ニュー容器B」ですよねっ?

もも
そ、そうですね。
(なんで、いい大人のごきげんとりやってんだか・・・)
では、いよいよ一番下の段の「横はたし算」をして、
式を立てていきますね。
(なんで、いい大人のごきげんとりやってんだか・・・)
では、いよいよ一番下の段の「横はたし算」をして、
式を立てていきますね。

もも
式は、



もも
両辺に分母の100があるから、はらってよさそうだな。
ということは、

答えは 150gです。
ということは、
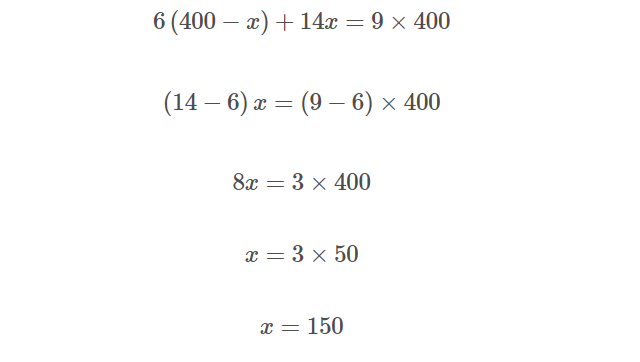
答えは 150gです。
こたえ

Lukia
いかがでしたか。今回と次回は、「2種類の濃度の食塩水を混ぜ合わせる」問題の仕上げとなります。
問題文が長い場合、このように小分けにして、できるところから考えていくという姿勢が大切になってきます。
問題文が長い場合、このように小分けにして、できるところから考えていくという姿勢が大切になってきます。
150g
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません