中学数学の2種類の濃度の食塩水を混ぜる問題(その7)

読了時間: 約5分35秒
[mathjax]

Lukia
さて、今回も「うっかりさん」の問題です。(笑)

もも
またぁ?
なんだって、こうも「うっかり」するんだか…。
なんだって、こうも「うっかり」するんだか…。

Lukia
ふふ。まぁ、そう言わずに。
さて、さっそく以下に問題を載せますので、いったんスクロールの手を止めて解いてみてくださいね。
さて、さっそく以下に問題を載せますので、いったんスクロールの手を止めて解いてみてくださいね。
問題
質量パーセント濃度が16%の食塩水と8%の食塩水を混ぜて、ある濃度の食塩水を作ろうとしたところ、
分量を逆にしたため、濃度が11%の食塩水が400gできてしまった。
本来作ろうとした食塩水の濃度は何%であったか。
分量を逆にしたため、濃度が11%の食塩水が400gできてしまった。
本来作ろうとした食塩水の濃度は何%であったか。
表に書き込む。

もも
中一でも、中二でも解ける問題だけど、
ひとまずは、表を作成するか。
横長の線を3本と、その線を4等分するように縦の線を3本引きます。
ひとまずは、表を作成するか。
横長の線を3本と、その線を4等分するように縦の線を3本引きます。

Lukia
ももちゃんは、下のような表を描いています。
次に、①から⑥をうめていきますよ。
次に、①から⑥をうめていきますよ。
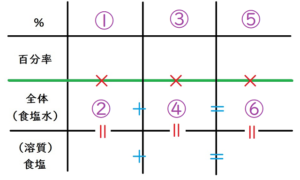
間違えて作った食塩水

もも
はい。
問題文からすると、濃度を表す数字が3つと、
間違えてできてしまった食塩水の重さが300ということがわかっています。
というわけで、
①が7、
③が16
⑤が13、
⑥が300となりますね。
問題文からすると、濃度を表す数字が3つと、
間違えてできてしまった食塩水の重さが300ということがわかっています。
というわけで、
①が7、
③が16
⑤が13、
⑥が300となりますね。

Lukia
はい。
それでは、②と④はどうしますか。
それでは、②と④はどうしますか。

もも
この表は、同じ列だと「縦はかけ算」で、
同じ段だと、「横はたし算」でした。
②+④=300
という式が成り立つので、
②を \(\Large x\) とすれば、
④は、\(\Large 300-x\) とあらわせます。
同じ段だと、「横はたし算」でした。
②+④=300
という式が成り立つので、
②を \(\Large x\) とすれば、
④は、\(\Large 300-x\) とあらわせます。
本来作ろうとした食塩水

Lukia
せっかくですから、「本来作ろうとした食塩水の濃度」を表せるような表も作成してみましょう。


もも
そうですね。似たような作業はまとめてやっておくほうが楽ですもんね。

もも
それに、問題文を読む限り、前回の問題と数字が違うだけで内容は一緒だから、
中一なら、いったん「それぞれ混ぜ合わせた食塩水の重さ」を出さないといけないけど、
中二で連立方程式を習っていたら、二つの表によって立てた式で、
一気に濃度が求められそうですもんね。
中一なら、いったん「それぞれ混ぜ合わせた食塩水の重さ」を出さないといけないけど、
中二で連立方程式を習っていたら、二つの表によって立てた式で、
一気に濃度が求められそうですもんね。

Lukia
くっ、おぬし、やるなッ・・・。

もも
はいはい。
じゃ、もう一つ表を描いて、数字をうめていきます。
①が7、
③が16なのは一緒で、
じゃ、もう一つ表を描いて、数字をうめていきます。
①が7、
③が16なのは一緒で、

もも
「分量を逆にした」とあるから、
どっちにしても、300gの食塩水になるということは変わらないんだな。
どっちにしても、300gの食塩水になるということは変わらないんだな。

もも
まず、⑥が300で、
最初に作った表と分量が逆なんだから、
②が \(\Large 300-x\) 、
④が \(\Large x\) となりますね。
最初に作った表と分量が逆なんだから、
②が \(\Large 300-x\) 、
④が \(\Large x\) となりますね。

Lukia
この表では、⑤がまだ空欄ですね。

もも
はい。
というわけで、「本来作ろうとした食塩水の濃度」を \(\Large y\) とおきます。
だから、⑤は \(\Large y\) です。
というわけで、「本来作ろうとした食塩水の濃度」を \(\Large y\) とおきます。
だから、⑤は \(\Large y\) です。

Lukia
ここからは、2つの表に共通する操作があれば、
一気にやってしまいます。
一気にやってしまいます。
%を百分率に直しておく。

もも
百分率に直すのは、簡単。
2つの表で、①と③は共通しています。
だから、①は、\(\Large \frac{7}{100}\)
③は \(\Large \frac{16}{100}\) とおけます。
2つの表で、①と③は共通しています。
だから、①は、\(\Large \frac{7}{100}\)
③は \(\Large \frac{16}{100}\) とおけます。

Lukia
そうですね。
そして、最初の表の⑤は、\(\Large \frac{13}{100}\) 、
あとの表の⑤は・・・。
そして、最初の表の⑤は、\(\Large \frac{13}{100}\) 、
あとの表の⑤は・・・。

もも
\(\Large \frac{y}{100}\) ですっ!

Lukia
たまには、いいとこ見せたいのに・・・。(涙)
縦はかけ算・横はたし算

Lukia
それでは、表の縦の列を計算していきましょうね。
今回は、2つの表があるので、見出しを2つにして、
それぞれやっていきましょう。
今回は、2つの表があるので、見出しを2つにして、
それぞれやっていきましょう。
最初の表(分量を逆にしてしまった食塩水)

もも
「縦はかけ算」でしたから、
それぞれかけ算をして、表の一番下の段のマスに書き込んでいきます。
それぞれかけ算をして、表の一番下の段のマスに書き込んでいきます。

もも
左から、
\(\Large \frac{7}{100}\times x\) 、
\(\Large \frac{16}{100}\times \left( 300-x\right)\) 、
\(\Large \frac{13}{100}\times 300\) となりますね。
\(\Large \frac{7}{100}\times x\) 、
\(\Large \frac{16}{100}\times \left( 300-x\right)\) 、
\(\Large \frac{13}{100}\times 300\) となりますね。
あとの表(本来作ろうとした食塩水)

もも
こちらも、最初の表とやることは一緒なので、
左から、
\(\Large \frac{7}{100}\times \left( 300-x\right)\) 、
\(\Large \frac{16}{100}\times x\) 、
\(\Large \frac{y}{100}\times 300\) となりますね。
左から、
\(\Large \frac{7}{100}\times \left( 300-x\right)\) 、
\(\Large \frac{16}{100}\times x\) 、
\(\Large \frac{y}{100}\times 300\) となりますね。
一番下の段の「たし算」をする。

Lukia
では、一番下の段の「横はたし算」をして、
2つの式を立ててみてください。
また、「最初の表」とか「あとの表」というのは、めんどくさいですから、
「最初の表」によって作られた式を①、
「あとの表」によって作られた式を②としてください。
2つの式を立ててみてください。
また、「最初の表」とか「あとの表」というのは、めんどくさいですから、
「最初の表」によって作られた式を①、
「あとの表」によって作られた式を②としてください。

もも
はい。
まず、最初の表の式が、
\(\Large \frac{7}{100}\times x+\frac{16}{100}\times \left( 300-x\right) =\frac{13}{100}\times 300\) ・・・① です。
まず、最初の表の式が、
\(\Large \frac{7}{100}\times x+\frac{16}{100}\times \left( 300-x\right) =\frac{13}{100}\times 300\) ・・・① です。

もも
あとの表の式が、
\(\Large \frac{7}{100}\times \left( 300-x\right)+\frac{16}{100}\times x =\frac{y}{100}\times 300\) ・・・② です。
\(\Large \frac{7}{100}\times \left( 300-x\right)+\frac{16}{100}\times x =\frac{y}{100}\times 300\) ・・・② です。
計算して答えを求める

Lukia
式を2つ立てたので、中一の人や、まだ連立方程式を習っていない人は、
「中一バージョン」を見てください。
また、案外簡単かもしれませんので、一応「中二バージョン(連立方程式)」も見てみると、
中一の人でも、楽に解けるかもしれません。
「中一バージョン」を見てください。
また、案外簡単かもしれませんので、一応「中二バージョン(連立方程式)」も見てみると、
中一の人でも、楽に解けるかもしれません。
中一バージョン

もも
まず、式①を計算します。
\(\Large \frac{7}{100}\times x+\frac{16}{100}\times \left( 300-x\right) =\frac{13}{100}\times 300\) ・・・①分母の100をはらうと、
\(\Large 7x+16\left( 300-x\right)=13\times 300\)\(\Large 7x-16x=\left( 13-16\right)\times 300\)\(\Large -9x=-3\times 300\)
\(\Large \frac{7}{100}\times x+\frac{16}{100}\times \left( 300-x\right) =\frac{13}{100}\times 300\) ・・・①分母の100をはらうと、
\(\Large 7x+16\left( 300-x\right)=13\times 300\)\(\Large 7x-16x=\left( 13-16\right)\times 300\)\(\Large -9x=-3\times 300\)
マイナスが気持ち悪いので、両辺を\(\Large -3\) でわって、
\(\Large 3x=300\) となり、
\(\Large x=100\) が求まります。

もも
これを式②に代入して、計算します。\(\Large \frac{7}{100}\times \left( 300-100\right)+\frac{16}{100}\times 100 =\frac{y}{100}\times 300\) ・・・②
こっちも分母の100をはらって、カッコ内の計算をすると、
\(\Large 7\times 200 + 16\times 100 = 300y\)
\(\Large \left( 7\times 2 +16\right)\times 100 = 3y\times 100\)
\(\Large 30=3y\)
\(\Large y=10\) が求まります。
中二バージョン(連立方程式)

Lukia
中二バージョン(連立方程式)は、ふきだしなしで書いてみますね。
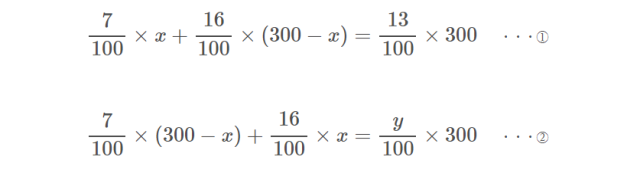
まず、どちらの式も分母の100をはらって、簡単な式に直します。
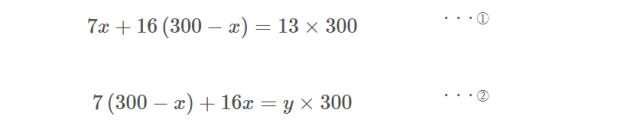
カッコをはずすため展開してみると、
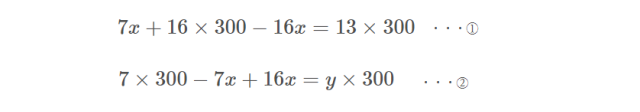
①と②の式の左辺は左辺同士、右辺は右辺同士でたし算をしてみます。
すると、


Lukia
「連立方程式」というほどの連立方程式でもないけれど、
中一の人は、学校の先生に「教えてないことはするな!」なんて言われても困るので、
めんどくさくても、中一バージョンでやるほうがいいかもしれませんね。
中一の人は、学校の先生に「教えてないことはするな!」なんて言われても困るので、
めんどくさくても、中一バージョンでやるほうがいいかもしれませんね。
こたえ
13%
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません