中学数学の2種類の濃度の食塩水を混ぜる問題(その5)

読了時間: 約3分45秒
[mathjax]

Lukia
・・・。体がだるいですね・・・。

もも
体調不良ですか?

Lukia
梅雨時期の雨が降る前日は、眠りが浅かったりするんですよね。
やっぱり、寄る年波でしょうか。(汗)
それに昨日は気になる数学があって、
寝てるんですけど、どうやって記事にしようか。と考えていたみたいです。
やっぱり、寄る年波でしょうか。(汗)
それに昨日は気になる数学があって、
寝てるんですけど、どうやって記事にしようか。と考えていたみたいです。

もも
考えながら寝るなんて、眠りが深いわけがないでしょ。

Lukia
そうですよね。
ま、とはいえ、今回もがんばっていきましょうね。
それでは、さっそく下に問題を示します。
スクロールの手を止めて、いったん解いてから、答え合わせしてみてください。
ま、とはいえ、今回もがんばっていきましょうね。
それでは、さっそく下に問題を示します。
スクロールの手を止めて、いったん解いてから、答え合わせしてみてください。
問題
6%の食塩水と3%の食塩水を混ぜて、5%の食塩水を780g作りたい。
6%と3%の食塩水をそれぞれ何g混ぜればよいか。
6%と3%の食塩水をそれぞれ何g混ぜればよいか。
表に書き込む。

もも
じゃ、ちゃちゃっと表を描きますね。
横長の線を3本と、
それを4等分するように縦に3本線を引きます。
横長の線を3本と、
それを4等分するように縦に3本線を引きます。

Lukia
ももちゃんは、以下のような表を描いています。
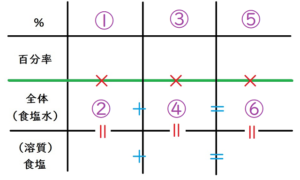

もも
次に問題を読みながら、縦の列をうめるように、表に数字を書き込んでいきます。

もも
6%の食塩水・・・
えっ、「6%の食塩水と3%の食塩水を混ぜて」??
どっちも、全体の重さが書いてない!!
これは、新しいタイプの問題ですね。
えっ、「6%の食塩水と3%の食塩水を混ぜて」??
どっちも、全体の重さが書いてない!!
これは、新しいタイプの問題ですね。

Lukia
そうですね。
ま、表の①から⑥は、どこが \(\Large x\) となってもおかしくないですもんね。
ま、表の①から⑥は、どこが \(\Large x\) となってもおかしくないですもんね。

もも
体がだるいわりに、難しい問題出すんだから。
ま、でも、まずはわかるところを確実に書き込むことが大事だから、
次に進みます。
ま、でも、まずはわかるところを確実に書き込むことが大事だから、
次に進みます。

もも
ひとまず、
①は6、
③は3 で・・・。
できあがりは、5%の食塩水が780gだから、
⑤が5、
⑥が780 か。
①は6、
③は3 で・・・。
できあがりは、5%の食塩水が780gだから、
⑤が5、
⑥が780 か。

もも
そして、前回、前々回ぐらいから、
「全体の重さ」の段の「横はたし算」を先にやってもいい。
っていわれているから、やってみようかな。

Lukia
前回までの内容が役に立っているみたいですね。

もも
はい。
じゃぁ、②を \(\Large x\) とおいて・・・。
じゃぁ、②を \(\Large x\) とおいて・・・。

Lukia
④は \(\Large y\) とか?

もも
\(\Large y\) ですか?
ってことは、
$$\Large x+y=780$$
となるけど、④は、
$$\Large y=780-x$$
になりますよね。
ってことは、
$$\Large x+y=780$$
となるけど、④は、
$$\Large y=780-x$$
になりますよね。

もも
あっ、別に④を \(\Large y\) とおく必要がないじゃないですか!

Lukia
あはは。ばれたか。(笑)
たしかに、②を \(\Large x\) 、④を \(\Large y\) とおいて、
連立方程式として解こうと思えば解けなくもないでしょう。
しかし、数学は、
「おいた文字の数だけ、式を立てなければならない。」
という絶対的なルールがありますので、一次方程式の範囲で解けるなら、そのほうがいいんですね。
中学校2年生になると、連立方程式を習うので、ついつい④を \(\Large y\) と置きたくなるんですが、極力文字を増やさないようにするほうが、楽に解けるんですよね。
たしかに、②を \(\Large x\) 、④を \(\Large y\) とおいて、
連立方程式として解こうと思えば解けなくもないでしょう。
しかし、数学は、
「おいた文字の数だけ、式を立てなければならない。」
という絶対的なルールがありますので、一次方程式の範囲で解けるなら、そのほうがいいんですね。
中学校2年生になると、連立方程式を習うので、ついつい④を \(\Large y\) と置きたくなるんですが、極力文字を増やさないようにするほうが、楽に解けるんですよね。

もも
わざとひっかけるなんて、ひどいぃ。
ま、でも、これで②が \(\Large x\) 、④が \(\Large 780-x\) とおけました。
ま、でも、これで②が \(\Large x\) 、④が \(\Large 780-x\) とおけました。
%を百分率に直しておく。

Lukia
表の①から⑥までがすべて埋まったので、
①、③、⑤の「%」を百分率に直していきます。
①、③、⑤の「%」を百分率に直していきます。

もも
はいは~い。これは、簡単だからすぐ終わります。
左から、$$\Large \frac{6}{100} ・ \frac{3}{100} ・ \frac{5}{100}$$です。
左から、$$\Large \frac{6}{100} ・ \frac{3}{100} ・ \frac{5}{100}$$です。
縦はかけ算・横はたし算

Lukia
こういうふうに手順化すると早いですよね。
それでは、一番下の段のマスをうめるために、「縦はかけ算」をしていきましょう。
それでは、一番下の段のマスをうめるために、「縦はかけ算」をしていきましょう。

もも
は~い。
左から、$$\Large \frac{6}{100}\times x ・ \frac{3}{100}\times\left( 780-x\right) ・ \frac{5}{100}\times 780$$です。
左から、$$\Large \frac{6}{100}\times x ・ \frac{3}{100}\times\left( 780-x\right) ・ \frac{5}{100}\times 780$$です。

Lukia
めっちゃ早いですね、ももちゃん・・・。

もも
そうですか?もう慣れました。
一番下の段の「たし算」をする。

Lukia
(慣れたって・・・。)
さ、それでは、一番下の段の「横はたし算」が残っていますので、
それを・・・。
さ、それでは、一番下の段の「横はたし算」が残っていますので、
それを・・・。

もも
$$\Large \frac{6}{100}\times x + \frac{3}{100}\times\left( 780-x\right) = \frac{5}{100}\times 780$$ですっ!

Lukia
ま、まだ言い終えてないのに・・・( ̄□ ̄;)
も、ももちゃん、聞いてます?
も、ももちゃん、聞いてます?

もも
聞いてますよ。
えっと、計算すると、
$$\Large x=520 , 780-x=260$$となるので、
6%の食塩水が、\(\Large 520 g\) 、
3%の食塩水が、\(\Large 260 g\) とわかりますね。
えっと、計算すると、
$$\Large x=520 , 780-x=260$$となるので、
6%の食塩水が、\(\Large 520 g\) 、
3%の食塩水が、\(\Large 260 g\) とわかりますね。

Lukia
うう、答えまで言われちゃった・・・。
んもう、正解ですッ!(涙)
んもう、正解ですッ!(涙)

もも
てへっ。
こたえ
6% 520g
3% 260g
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません