中学数学の2種類の濃度の食塩水を混ぜる問題(その4)

読了時間: 約3分13秒
[mathjax]

Lukia
それでは、今回もがんばっていきましょうね。
今回の問題は以下のとおりです。
今回の問題は以下のとおりです。
問題
濃度3%の食塩水A 500gに、ある濃度の食塩水Bを混ぜ合わせたら、濃度5%の食塩水が700gできた。
食塩水Bの濃度は何%であったか。
食塩水Bの濃度は何%であったか。
表に書き込む。

もも
えっと、横長の線を3本引いて、
その横長の線を4等分するように、3本の縦の線を引くんでした。
その横長の線を4等分するように、3本の縦の線を引くんでした。

Lukia
そうでしたね。
ももちゃんは、以下のような表を描いています。
ももちゃんは、以下のような表を描いています。
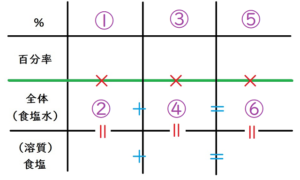

もも
次に、問題文にある数字を表に書き込んでいきます。
3%の食塩水が500gだから、
①に3、
②に500を書き込みます。
3%の食塩水が500gだから、
①に3、
②に500を書き込みます。

Lukia
そうですね。

もも
次が・・・。
あれっ、「ある濃度の食塩水B」?
濃度はわからないんだ・・・。
たぶん、ここが \(\Large x\) になるんだろうな。
あれっ、「ある濃度の食塩水B」?
濃度はわからないんだ・・・。
たぶん、ここが \(\Large x\) になるんだろうな。

もも
えっ、食塩水Bは、重さも書いてない!?

Lukia
新しいパターンですよね。

もも
ま、でも、ひとまず、わかるところを書き込んでいくのが大事だから、
③と④には書き込まずに、先に進みます。
5%の食塩水が700gできた。とあるから、
⑤が5、
⑥が700ということになりますね。
③と④には書き込まずに、先に進みます。
5%の食塩水が700gできた。とあるから、
⑤が5、
⑥が700ということになりますね。

Lukia
そろそろ慣れてきていると思いますので、
全体の重さの段の「横はたし算」を先にやってみましょうか。
そうすれば、③と④が埋まりますからね。
全体の重さの段の「横はたし算」を先にやってみましょうか。
そうすれば、③と④が埋まりますからね。

もも
全体の重さの段の「横はたし算」?
②+④=⑥ が成り立つはずだから、
④=⑥-②か。
ということは、$$\Large 700-500$$ だから・・・。
②+④=⑥ が成り立つはずだから、
④=⑥-②か。
ということは、$$\Large 700-500$$ だから・・・。

もも
④は、200だ!

Lukia
表に書き込んでいくことで、こういう計算も途中で簡単に行えるようになりますね。
さて、問題文の最後に、「食塩水Bの濃度は何%であったか。」とありますから、
③に \(\Large x\) が入ることになりますね。
さて、問題文の最後に、「食塩水Bの濃度は何%であったか。」とありますから、
③に \(\Large x\) が入ることになりますね。

もも
あ、そういえば、前回も「横はたし算」を先にやりましたよね。
ということは、
全体の重さの段の「横はたし算」は、表に書き込みながらやれば、
時短になるってことですね。
ということは、
全体の重さの段の「横はたし算」は、表に書き込みながらやれば、
時短になるってことですね。

Lukia
四則計算だと、かけ算をしてからたし算という順番ですが、
この食塩水の表に関しては、たし算より先にかけ算ができるパターンの問題は
少ないと思っていていいと思います。(今のところね。)
この食塩水の表に関しては、たし算より先にかけ算ができるパターンの問題は
少ないと思っていていいと思います。(今のところね。)
%を百分率に直しておく。

もも
表がひとまず埋まりました。
次は、「%を百分率に直す」んだったな。
①が \(\Large \frac{3}{100}\) 、
③が \(\Large \frac{x}{100}\)、
⑤が \(\Large \frac{5}{100}\)です。
次は、「%を百分率に直す」んだったな。
①が \(\Large \frac{3}{100}\) 、
③が \(\Large \frac{x}{100}\)、
⑤が \(\Large \frac{5}{100}\)です。

Lukia
手慣れてきましたね。では、次にいきましょう。
縦はかけ算・横はたし算

もも
3%の食塩水の列は、
$$\Large \frac{3}{100}\times 500$$
$$\Large \frac{3}{100}\times 500$$

もも
\(\Large x\)% の食塩水の列は、
$$\Large \frac{x}{100}\times 200$$
$$\Large \frac{x}{100}\times 200$$

もも
5%の食塩水の列は、
$$\Large \frac{5}{100}\times 700$$
$$\Large \frac{5}{100}\times 700$$
でした。
一番下の段のたし算をする。

Lukia
それでは、式を立ててみましょう。

もも
はい。
$$\frac{3}{100}\times 500 + \frac{x}{100}\times 200 = \frac{5}{100}\times 700$$
$$\frac{3}{100}\times 500 + \frac{x}{100}\times 200 = \frac{5}{100}\times 700$$
です。

Lukia
そうですね。
そして、今回はよく見てみると、各項の分母・分子に100がありますので、
無視してよいことになりますね。
ちなみに、ひとつでもそろわなかったら、無視しちゃだめですよ。
そして、今回はよく見てみると、各項の分母・分子に100がありますので、
無視してよいことになりますね。
ちなみに、ひとつでもそろわなかったら、無視しちゃだめですよ。

Lukia
$$3 \times 5 + x \times 2 = 5 \times 7$$
を計算すればよいことになりますね。
\(\Large x=10\) が出ましたか?
を計算すればよいことになりますね。
\(\Large x=10\) が出ましたか?

もも
はい。
つまり、Bの食塩水の濃度は、
\(\Large 10\) %ということになりますね。
つまり、Bの食塩水の濃度は、
\(\Large 10\) %ということになりますね。

Lukia
よくできました。
おわりに

Lukia
表を書き込んで解くやり方には慣れてきたでしょうか。
「全体の重さの段」の「横はたし算」は、場合によっては先にやってしまってもいいということを覚えると、より早く解けるようになることがわかりましたね。
「全体の重さの段」の「横はたし算」は、場合によっては先にやってしまってもいいということを覚えると、より早く解けるようになることがわかりましたね。
こたえ
10%
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません