中学数学の食塩水「とりだし」問題（その1）

2018年7月12日2023年1月15日食塩水の濃度実用数学技能検定（数学検定数検),数検3級

読了時間: 約7分29秒

今回から三回にわたって、「とりだし」問題をやっていこうと思います。
「とりだし」問題というのは、私が名付けたもので、数学の教科書などにこういう名前の問題があるわけではありません。
一見難しそうですが、問題文でポイントを押さえれば、式を機械的に立て、解けるようになりますよ。 [mathjax]

問題

16%の食塩水180gから食塩水30gを捨て、水を50g加える。
さらに、食塩水50gを捨て、水50gを加えた。
この食塩水の濃度は何％になったか。

表に書き込む。

もも

う～ん、なんだか難しそうですねぇ。
食塩水を取り出しては、水を入れ・・・ということをくりかえすなんて、
なんだかこんがらがっちゃうなぁ。

Lukia

何がわからなくて、こんがらがっちゃうと思いますか。

もも

水を入れるから、濃度が変わっちゃいますよね。
濃度がわからないから、こんがらがっちゃうのかなぁ。

Lukia

そうです。濃度が変わっていきますね。
しかし、変わらないものもありますので、問題を解きながらポイントをつかんでいきましょう。
それでは、まず、いつもどおり表を描いて、式を立てていきましょう。
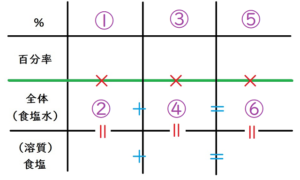
まずは、問題文の2行目までの表を作成しましょう。

もも

まずは、横長の線を3本と、それを4等分するように縦の線を3本引きますね。

Lukia

ももちゃんは、以下のような表を描いています。

もも

問題文を読みながら、表に数字を書き込んでいきます。
まずは、濃度の段を埋めていきます。
①は16ですね。
水を加えるから、③は0　です。

Lukia

ここは、これまでに何度もやっていますから、さっと書き込めますね。
それでは、問題文を見ながら、②と④を入れてみてください。

もも

はい。
食塩水はもともと180ｇあったけど、30ｇ捨てたとあるから、
②は$\Large 180-30=150$ となり、
150 と書き込みます。
④は50ですね。

もも

食塩水に水を加えれば、その濃度は、もとの16％のままでいられませんから、
$\Large x$ とおけばよいと思います。
ゆえに、⑤は $\Large x$ ですね。
次に、②+④=⑥となりますから、
⑥は、$\Large 150+50=200$ より、
200 を書き込みます。

％を百分率に直しておく。

もも

％を百分率に直すのは簡単。
左から、 $\Large \frac{16}{100}$ ・ $\Large \frac{0}{100}$ ・ $\Large \frac{x}{100}$ となります。

Lukia

水の $\Large \frac{0}{100}$ が気持ち悪い人は、
この段階で、シンプルに $\Large 0$ としてもよいですよ。

式を立てる。

Lukia

これまでは、細かく段取りをしていましたが、もうそろそろ慣れていると思いますので、
「縦はかけ算・横はたし算」をして、式を立てていきましょう。

もも

表の縦の列は、かけ算をし、表の一番下の段のマスをうめていきます。
そして、表の一番下の段を「横はたし算」をすれば、式が立てられます。

もも

式は、
$\Large \frac{16}{100}\times 150=\frac{x}{100}\times 200$ となりますね。

途中の濃度は求めなくてもOK。

もも

じゃぁ、$\Large x$ を求めていこうかな。

Lukia

いやいや、ももちゃん、待ってください。
$\Large x$ の具体的な数字がいくらかわかる必要がありますか？

もも

いや、あんまりないかな。
でも、次の問題を解くときには必要なのでは？

Lukia

たしかに、次の問題を解くときに、$\Large x$ は必要なのですが、
式変形をしていけば消えるので、具体的な数字を出す必要がないんですね。
$\Large \frac{x}{100}$ を左辺に置くような式変形はできますか？

もも

あ、それはできます。

$$\Large \frac{x}{100}\times 200=\frac{16}{100}\times 150$$
両辺を200でわって、
$$\Large \frac{x}{100}=\frac{16}{100}\times \frac{150}{200}$$
$$\Large \frac{x}{100}=\frac{16}{100}\times \frac{3}{4}$$

Lukia

そうですね。
では、この式を①としておきましょう。
$\Large \frac{x}{100}=\frac{16}{100}\times \frac{3}{4} ・・・①$

「さらに、」以下の式を立てる。

Lukia

では、問題文の2行目にある、「さらに、」以下の操作の式を立てていきましょう。

もも

表に書き込んでいくと、
①は $\Large x$ 、
③は $\Large 0$ 、
②は、$\Large 200-50=150$ だから、$\Large 150$ で、
④は $\Large 50$ です。

Lukia

そうですね。
⑤と⑥はどうなりますか。

もも

$\Large x$ ％の食塩水に水を加えたのですから、$\Large x$ ％のままではないはず。
もうすでに、$\Large x$ は使ってしまったので、
$\Large y$ とおくことにします。
だから、⑤は $\Large y$ ですね。
⑥は、②と④を足したものですから、$\Large 200$ です。

Lukia

では、%を百分率に直し、表の「縦はかけ算・横はたし算」をして、
式を立ててください。

もも

はい。
$\Large \frac{x}{100}\times 150=\frac{y}{100}\times 200$ となります。

Lukia

この式を②とします。
このままで、①を代入してもよいのですが、
②も、左辺を $\Large \frac{y}{100}$ として式変形してみてください。

$$\Large \frac{y}{100}\times 200=\frac{x}{100}\times 150$$
両辺を200でわって、
$$\Large \frac{y}{100}=\frac{x}{100}\times \frac{150}{200}$$
$$\Large \frac{y}{100}=\frac{x}{100}\times \frac{3}{4} ・・・②$$

②式に①を代入してこたえを求める。

Lukia

式変形をした②に①を代入して、こたえを求めてみましょう。

$$\Large \frac{x}{100}=\frac{16}{100}\times \frac{3}{4}・・・①$$
$$\Large \frac{y}{100}=\frac{x}{100}\times \frac{3}{4}・・・②$$
①を②に代入して、
$$\Large \frac{y}{100}=\frac{16}{100}\times \frac{3}{4}\times \frac{3}{4}$$
$$\Large \frac{y}{100}=\frac{16}{100}\times \frac{9}{16}$$
$$\Large \frac{y}{100}=\frac{9}{100}$$
$$\Large y=9$$

もも

最終的に9％の食塩水になりました。

もうちょっと簡単に解けないか。

Lukia

実は、この「とりだし」問題、あと二問ひかえているんですが、
この操作を、毎度やるのはちょっと大変じゃないですか？

もも

そうですねぇ。
どうしても解けないときは、表を二つ描いて、式を立てていけばいいけれど、
簡単にできる方法があるなら、ぜひ知りたいし、
それをあとの二問で試してみたいです。

Lukia

①式と②式を見て、気づくことはありませんでしたか？

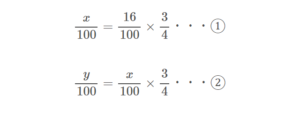
もも

$\Large \frac{3}{4}$ が共通してかけられていました。

Lukia

この $\Large \frac{3}{4}$ は、$\Large \frac{150}{200}$ を約分したものでした。
では、この $\Large \frac{150}{200}$ は、何分の何ですか？

もも

$\Large \frac{もとの食塩水の重さ}{新しい食塩水の重さ}$ です。

Lukia

その通り。
あらためて問題文を読んでもらうと、
水を混ぜ合わせる前の食塩水の重さは、今回だと必ず $\Large 150$ ｇにしてあって、
そこに必ず水を $\Large 50$ ｇ加えるので、
できあがる食塩水は、濃度こそ違いますが、全体の重さは必ず $\Large 200$ ｇになっているんですね。

もも

わっ、ホントだ！

Lukia

つまり、問題文を読んで、捨てる食塩水の重さと、加える水の重さが同じ「とりだし」問題だったら、
以下の式を立てればよさそうですね。

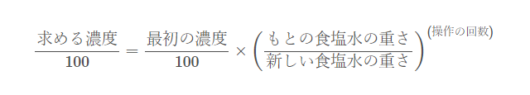
Lukia

今回の問題の数字をあてはめてみてください。
求める濃度は、上と対応しやすいよう、 $\Large y$ としておきましょう。

もも

はい。
「求める濃度」が $\Large y$ で、
「最初の濃度」が $\Large 16$ 、
「もとの食塩水の重さ」は常に $\Large 150$ gで、
「新しい食塩水の重さ」は、水を50ｇ加えて、常に $\Large 200$ gでした。
そして、その操作を $\Large 2$ 回繰り返していますから・・・

$$\Large \frac{y}{100}=\frac{16}{100}\times \left( \frac{150}{200}\right)^2$$
両辺の分母の100を払い、約分をして、
$$\Large y=16\times \left( \frac{3}{4}\right)^2$$
$$\Large y=16\times \frac{9}{16}$$
$$\Large y=9$$

もも

あっ、ちゃんとこたえが出ました！

Lukia

そうですね。
この式を覚えて、問題文を丁寧に読んで、数字をあてはめていけば、
表を描くことなく、一気に問題が解けそうですね。

こたえ

Lukia

いかがでしたか。
一種のテストあるあるだと思いますが、
問題用紙のほとんどは、解答作成のための下書きや計算スペースがあまり用意されていないですよね。
いつものように、表を描き、丁寧に立式していけば、必ず解くことができますが、
難しい問題の場合は、案外このようにパターン化（公式化）して、何度も練習するうちに、
突然ストン！と理解できるようになることがあります。
時短できそうなところはないか。と考えながら問題を解いてみるのもいいかもしれませんね。