中学数学の2種類の濃度の食塩水を混ぜる問題(その2)

読了時間: 約3分5秒
[mathjax]

Lukia
さぁ、それでは今回もがんばって解いてみましょう。
まずは、問題をお見せしますね。
前回の内容を踏まえて、解けるかどうか試してみてください。
まずは、問題をお見せしますね。
前回の内容を踏まえて、解けるかどうか試してみてください。
問題
濃度が5%の食塩水200gと濃度が15%の食塩水を混ぜ合わせると濃度が11%の食塩水ができた。
15%の食塩水は何g混ぜ合わせたか。
15%の食塩水は何g混ぜ合わせたか。

もも
えっと・・・。まず、横長の線を3本と、その横長の線を4等分するように、
縦の線を3本引くんでした。
一番左の縦の列に、%・百分率・全体・食塩と書き込んで。。。
縦の線を3本引くんでした。
一番左の縦の列に、%・百分率・全体・食塩と書き込んで。。。

Lukia
うわ、ももちゃん、すごい記憶力ですね。
みなさんには、一応、表をお見せしましょうね。
みなさんには、一応、表をお見せしましょうね。
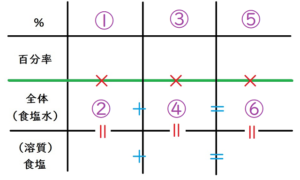

もも
前回の手順をもとに思い出しました。
あとは、問題文に書いてある数字をあてはめていけばいいんだったよな・・・。
今回も、数字は4つあるので、それを書き込んで・・・。
あとは、問題文に書いてある数字をあてはめていけばいいんだったよな・・・。
今回も、数字は4つあるので、それを書き込んで・・・。

Lukia
はい。縦の列に「ひとつの食塩水」について書くのを忘れないでね。

もも
はい。
①が5、
②が200、
③が15、
①が5、
②が200、
③が15、

もも
④が・・・あれっ?書いてない!

Lukia
そうですね。問題文を最後まで読むと、「15%の食塩水を何g混ぜ合わせたか。」とありますから、ここがわかってない、つまり、答えになるところですよね。
ということは、どうおけばよいですか?
ということは、どうおけばよいですか?

もも
\(\Large x\) です!

Lukia
そのとおりです。
では、⑤と⑥に進みましょう。
では、⑤と⑥に進みましょう。

もも
⑤は11です。

もも
⑥は・・・
たしか、横はたし算でしたよね。ということは、
$$\Large200+x $$
たしか、横はたし算でしたよね。ということは、
$$\Large200+x $$
でいいのかな?

Lukia
そうですね。
表に書き込む最中に、たし算ができそうならばしてしまいましょう。
ただ、慣れるまでは、「上の段から確実にうめていく」というルールだけは守ったほうがよいと思います。
せっかく表を作っても、手順がごちゃごちゃになったら意味がありませんからね。
表に書き込む最中に、たし算ができそうならばしてしまいましょう。
ただ、慣れるまでは、「上の段から確実にうめていく」というルールだけは守ったほうがよいと思います。
せっかく表を作っても、手順がごちゃごちゃになったら意味がありませんからね。

もも
はい。
じゃ、次は、百分率か。
「百分の」とすればいいんだから、
左から、
$$\Large\frac{5}{100}・\frac{15}{100}・\frac{11}{100}$$
じゃ、次は、百分率か。
「百分の」とすればいいんだから、
左から、
$$\Large\frac{5}{100}・\frac{15}{100}・\frac{11}{100}$$
とすればいいですね。

Lukia
まっ、まぶしいですっ、ももちゃん・・・。

もも
ふふん。
じゃ、次は、縦の列をかけ算していきます。
5%の列は、
$$\Large\frac{5}{100}\times200$$15%の列は、
$$\Large\frac{15}{100}\times x$$
11%の列は、
$$\Large\frac{11}{100}\times\left( 200+x\right)$$
ですっ。
じゃ、次は、縦の列をかけ算していきます。
5%の列は、
$$\Large\frac{5}{100}\times200$$15%の列は、
$$\Large\frac{15}{100}\times x$$
11%の列は、
$$\Large\frac{11}{100}\times\left( 200+x\right)$$
ですっ。

Lukia
ああっ、先生、よろよろしちゃいますっ。

もも
なんでですか?

Lukia
ええっ? だって、ももちゃんの成長が著しすぎて・・・。

もも
では、そこでよろよろしといてください。(笑)一番下の段のマスがうまったので、あとは、たし算でつなぐ。と。
式は、
$$\Large\frac{5}{100}\times200 + \frac{15}{100}\times x =\frac{11}{100}\times\left( 200+x\right)$$となりますね。
式は、
$$\Large\frac{5}{100}\times200 + \frac{15}{100}\times x =\frac{11}{100}\times\left( 200+x\right)$$となりますね。

Lukia
よろよろ・・・。

もも
Lukia先生のことは、ほっといて先に進みましょう。式は百分率を使って、ていねいに表したけど、
実際の計算は、
$$\Large 5\times200 + 15\times x = 11\left( 200+x\right)$$
でも問題ないんでした。
実際の計算は、
$$\Large 5\times200 + 15\times x = 11\left( 200+x\right)$$
でも問題ないんでした。

もも
計算すると・・・。
$$\Large 1000 + 15x = 2200 + 11x$$
$$\Large x = 300$$となります。
つまり、15%の食塩水は、\(\Large 300g\)混ぜたことになります。
$$\Large 1000 + 15x = 2200 + 11x$$
$$\Large x = 300$$となります。
つまり、15%の食塩水は、\(\Large 300g\)混ぜたことになります。

Lukia
ももちゃん、答えまで出しちゃったんですか?

もも
はい。もう終わっちゃいましたよ。

Lukia
ううっ・・・。
次回は、もっと難しい問題出してやるっ・・・。(ガクッ)
次回は、もっと難しい問題出してやるっ・・・。(ガクッ)

もも
Lukia先生はああいってますから、食塩水の問題はまだまだ続きそうですね。
こたえ
300g[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません