中学数学の2種類の濃度の食塩水を混ぜる問題

2018年6月14日2023年1月15日食塩水の濃度数検3級

読了時間: 約5分15秒

[mathjax]

Lukia

さぁ、それではいよいよ解いてみましょう。

もも

はい。（ちょっと心配だな。）

Lukia

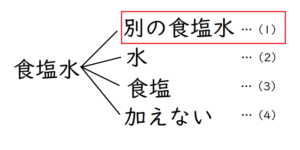
前回、食塩水の問題は、加えるものによって3パターンに分けられると話しましたね。

もも

はい。
えっと、「別の濃度の食塩水」と、「水」と、「食塩」でしたよね。

Lukia

おっ、よく覚えてますね。
早速今回から、「別の濃度の食塩水」を加える問題をやってみましょう。

問題

濃度2％の食塩水500gと濃度9%の食塩水200gを混ぜてできる食塩水の濃度は何％であるか。

もも

うわ～、％とｇがいっぱい。。。

Lukia

たしかに、単位が2種類あるから難しそうですね。
では、前回紹介した表を使って解いてみましょう。慣れたら自分ではしょったりしてもかまいませんが、
最初は、横長の線を3本と、その横長の線を4等分できるように、縦の線を3本入れます。

もも

線を縦横、3本ずつ引けばいいんですね。
よし、やってみよう。。。

Lukia

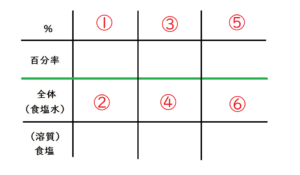
イメージとしては以下のようになりますね。

Lukia

一番左の列は、単位などの項目を書き込むところなので、
試験中のように急いでいるときや、問題そのものに慣れてきたら書く必要がなくなってきますよね。
つまり、慣れてきたら、縦の線を2本にして、横長の線を3等分すればいいことになってきます。

もも

そうなんだぁ。じゃ、線の本数を少なくできるようにがんばりたいです。

Lukia

さらに、本当は横長の線も2本にできます。
ただし、学校の定期試験や入試などでは、式を書きなさい。といわれることもありますし、ここにきてくれる人たちの理解度もまちまちでしょうから、省略せずていねいに書くことにしておきます。

もも

わかりました。

Lukia

さ、それではいよいよ、表に数字を書き込んでいきます。
問題文を読むと、いま、4つの数字が書かれていますね。これらを①～⑥にあてはめてみましょう。また、食塩水の濃度や重さは、縦に並べて書くようにしましょう。
つまり、横は別の食塩水の濃度や重さを書くことになりますね。

もも

えっと、まずは「2％の食塩水が500ｇ」か。
①に2％、②に500ｇでいいですか？

Lukia

いいですよ。次に進んでください。

もも

は～い。
じゃ、③は9％で、④は500ｇですね。
4つの数字を書き込めました。

Lukia

はい。では、⑤と⑥が残りましたね。
さて、あらためて問題文を読んでほしいのですが、今回は何を求めるのでしょうか。

もも

えっと・・・。
「食塩水の濃度は何％か。」とあるから、濃度ですか？

Lukia

そうですね。ということは、⑤に $ \LARGE x$ を書き込めばいいことになりますね。
ちなみに、⑥は計算するときにうまりますので、今は空欄のままでいいですよ。

もも

じゃ、⑤に $\LARGE x$ を書き込んで。と。
次は何ですか？

Lukia

次は、％を「百分率」に直します。
ここは、式を立てなさい。という指示がなければ、飛ばしてもいいところなのですが、
この講義ではていねいにやりたいので、書き込んでいきますよ。
それでは、ももちゃん、2％って、分数に直すと「なんぶんのなに」でしたっけ。

もも

えっと・・・。
$\Large\frac{2}{100}$ かな？

Lukia

そうです。そのとおり。
9％を百分率に直すと、
$\LARGE \frac{9}{100}$ ということになりますね。
それでは、$\LARGE x$％は？

もも

$\LARGE \frac{x}{100}$ ですか？

Lukia

そうです。具体的な数字がわからないため、$\Large x$ と置いていますから、
分数に直しても、$\Large \frac{x}{100}$ のようになります。
中学数学以降は、分子や分母にこのような文字が置かれることが増えてきますよ。

もも

はい。ちょっと安心しました。
それでは、次をお願いします。

Lukia

はい。実は、もう仕上げの一歩手前まできています。
今から、計算するための式を立てていくのですが、この表にはルールがあります。
「縦はかけ算・横はたし算」です。

もも

「縦はかけ算・横はたし算」ですか？

Lukia

はい。食塩水の濃度の問題は、実は、
食塩水に含まれている「食塩」の重さがいくらかを知るための式が立てられています。水に一定の割合で食塩が溶けているとして、全体の重さが100ｇ以外のとき、食塩はいったいいくら溶けているのか。というのを知りたいなら、百分率と全体の重さをかけ合わせればわかるようになっています。

もも

う～ん、なんだか難しい・・・。

Lukia

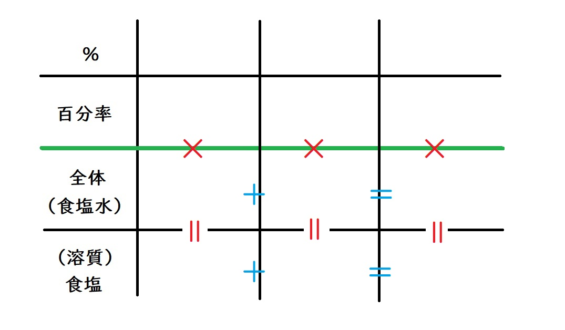
大丈夫。今から食塩水の問題を山ほど解いていけば、感覚的にわかってきますよ。さて、先ほど言ったルールを表に書き込むと、以下のようになります。

Lukia

まずは、縦のかけ算をして、2％と、9％の一番下の段を埋めてみましょう。

もも

えっと・・・。
2％の食塩水の列の一番下は、
$$\LARGE \frac{2}{100}\times500$$

ですね。

Lukia

いいですねぇ。では9％の食塩水の列もやってみてください。

もも

はい。
縦にかけ算をするのだから・・・。
$$\LARGE \frac{9}{100}\times200$$

となります。

Lukia

では、横のたし算をしましょう。
いま、⑥が空欄となっていますが、同じ段でたし算をすれば求められますね。

もも

$\LARGE 500+200$で、$\LARGE 700$ ですね。

Lukia

そうです。ということは、$\LARGE x$％の列も求められますね。

もも

あっ、ホントだ！
$$\LARGE \frac{x}{100}\times700$$

ですね。

Lukia

はい。それでは、いよいよ最後です。
一番下の段のたし算が残っていましたね。
そこが、試験などで書くべき式となりますので、書いてみてください。

もも

はい。
$$\LARGE \frac{2}{100}\times500 + \frac{9}{100}\times200 = \frac{x}{100}\times700$$

です。

Lukia

グッジョブです！
あとは、工夫して計算していくと、答えが出ますね。

もも

結局、
$$\LARGE 2\times 5 + 9\times 2 = 7x$$

を解けばいいことになりますね。

これを計算すると、$\LARGE x=4$だから、4％だ！

Lukia

正解です。
正式な式を立てるため、表にはきちんと百分率で表し、式にも書き込みましたが、
さっと計算するなら、％のままの
$$\LARGE 2\times500 + 9\times200 = x\times700$$
でもいいですよね。
まだ初回なので、どこがショートカットできるか。というのをつかむのは難しいかもしれませんが、これからたくさんの問題をこなすうちに、感覚的に理解できるようになると思います。

もも

はい。似たような問題を解いて、慣れていきたいです♪