tan θ（タンジェントシータ）を微分する。

2018年9月22日2023年1月15日微分とその応用実用数学技能検定（数学検定 数検),数検準1級

$$\begin{align}\left( \tan \theta\right)’=&\left( \frac{\sin \theta}{\cos \theta}\right)’
\\ =&\frac{\left( \sin \theta\right)’\cos \theta-\sin \theta\left( \cos \theta\right)’}{\left( \cos \theta\right)^2}\end{align}$$

Lukia

\(\sin \theta　や\cos \theta\)の微分・積分の問題を解く際には、
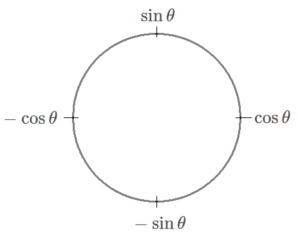
簡単でいいので、下のような図を描いておきましょう。
ちなみに、時計回りが「微分」で、
反時計回りが「積分」です。

tanθの微分（その1）

$$\begin{align}\left( \tan \theta\right)’=&\frac{\left( \sin \theta\right)’\cos \theta-\sin \theta\left( \cos \theta\right)’}{\left( \cos \theta\right)^2}
\\\\ =&\frac{\cos^{2} \theta+\sin^{2} \theta}{\cos^{2} \theta}
\\\\ =&\frac{1}{\cos^{2} \theta} \end{align}$$

tanθの微分（その2）

$$\begin{align}\left( \tan \theta\right)’=&\frac{\cos^{2} \theta+\sin^{2} \theta}{\cos^{2} \theta}
\\\\ =&\frac{\cos^{2} \theta}{\cos^{2} \theta}+\frac{\sin^{2} \theta}{\cos^{2} \theta}
\\\\ =& 1+\tan^{2} \theta\end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。