定義域が移動する放物線の最大値・最小値（下に凸）
読了時間: 約1分35秒
放物線（二次関数）の最大値・最小値を求める問題は、なかなか厄介に感じると思います。
今回は、下に凸の放物線について、定義域が移動する場合の最大値と最小値をまとめてみます。
放物線の式を
\( \ y=f\left( x\right)=a\left( x-\gamma\right)^2+c \ \)とし、
定義域を\( \ \beta \leqq x \leqq \alpha \ \) とします。
\( \ a \ , \ \gamma \ , \ c \ , \ \beta \ , \ \alpha \ \) はいずれも実数であり、
特に\( \ a \gt 0 \ , \ \beta \lt \alpha \ \) とします。
| 最大値 | 最小値 | |
 |
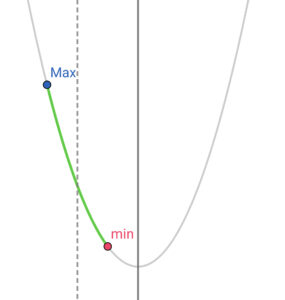\( \ \displaystyle\frac{\alpha+\beta}{2} \leqq \gamma \ \) のとき （定義域の中央が軸を含めて左側にあるとき） \( \ f\left( \beta\right) \ \) （左端）が最大値 |
\( \ \alpha \lt \gamma \ \) のとき （定義域の右端よりも右側に軸があるとき） \( \ f\left( \alpha\right) \ \) （右端）が最小値 |
 |
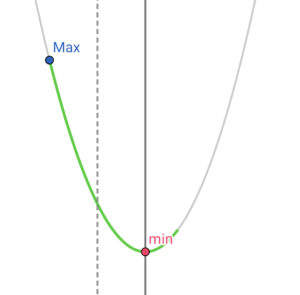\( \ \beta \lt \gamma \lt \alpha \ \) のとき （軸が定義域に含まれるとき） \( \ f\left( \alpha\right) \ \) （軸）が最小値 |
|
 |
||
|
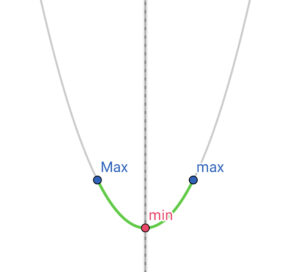\( \ \displaystyle\frac{\alpha+\beta}{2} \geqq \gamma \ \) のとき （定義域の中央が軸を含めて右側にあるとき） \( \ f\left( \alpha\right) \ \) （右端）が最大値 |
||
 |
||
 |
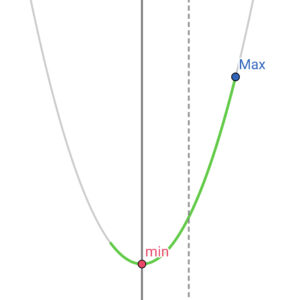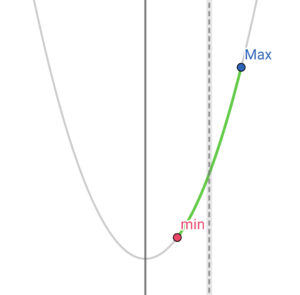\( \ \gamma \lt \beta \ \) のとき （軸が定義域の左端よりも右側にあるとき） \( \ f\left( \beta\right) \ \) （左端）が最小値 |
Lukia
余談ですが、これを私自身が学んだときは、黒板に書かれていたので、横に5つの放物線を並べられていました。
ブログで記事を書くときも、ごく最近まで横に5つの放物線を並べようとしていましたが、
ブログは縦長のメディアなので、そもそも無理だったんですよね。
（長らく気づかなかった・・・）
放物線を縦に並べると、定義域の移動がわかりやすいですね。
これはこれでアリですな。
ブログで記事を書くときも、ごく最近まで横に5つの放物線を並べようとしていましたが、
ブログは縦長のメディアなので、そもそも無理だったんですよね。
（長らく気づかなかった・・・）
放物線を縦に並べると、定義域の移動がわかりやすいですね。
これはこれでアリですな。
共有:
プロフィール
Author Profile