三角関数の値の大小関係（その2）【大学入学共通テスト2023年数学ⅡB】

2023年1月24日三角関数,大学入学共通テスト

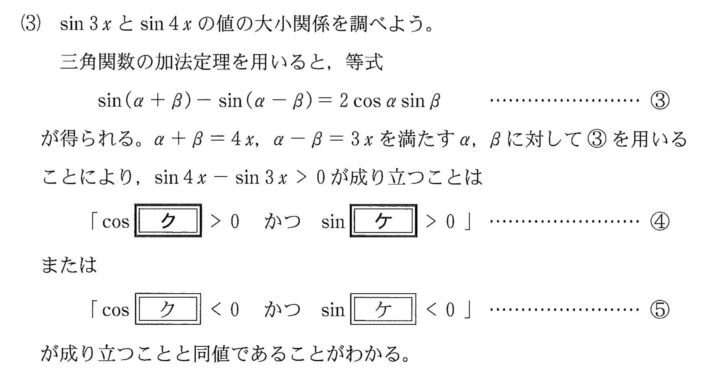連立方程式を解いて、\( \ \alpha \ , \ \beta \ \) を明らかにする。
\( \ \begin{eqnarray} \left\{ \begin{array}{l} \alpha + \beta = 4x \\ \alpha – \beta = 3x \end{array} \right. \end{eqnarray} \ \)
\( \ \begin{eqnarray} \left\{ \begin{array}{l} \alpha = \displaystyle\frac{7}{2}x \\ \beta = \displaystyle\frac{1}{2}x \end{array} \right. \end{eqnarray} \ \)

これより、③は
\( \ \sin 4x-\sin 3x=2\cos \displaystyle\frac{7}{2}x\sin \displaystyle\frac{1}{2}x \ \) と表せる。
よって、
$$\begin{align}\sin 4x-\sin 3x=2\cos \frac{7}{2}x\sin \frac{1}{2}x \gt &0 \\\\ \\\\ \cos {\color{#0004fc}{\frac{7}{2}x}} \gt 0&{\rm{かつ}} \ \sin {\color{#0004fc}{\frac{1}{2}}} {\color{#0004fc}{x}}\gt 0 \ \cdots \ {\rm{④}} \\\\ または\quad \quad \quad \quad &\\\\ \cos {\color{#0004fc}{\frac{7}{2}x}} \lt 0&{\rm{かつ}} \ \sin {\color{#0004fc}{\frac{1}{2}x}} \lt 0 \ \cdots \ \rm{⑤}\end{align}$$ 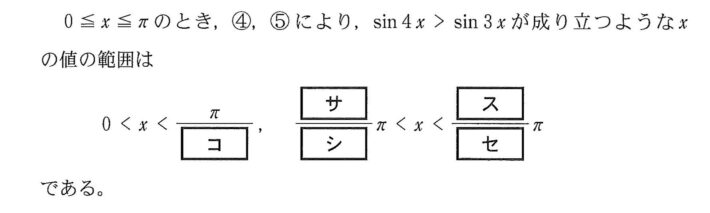$$\begin{align}0 \leqq &x \leqq \pi \\\\ 0 \leqq &\frac{1}{2}x \leqq \frac{ \pi }{ 2} \\\\ 0 \leqq &\sin \frac{1}{2}x \leqq 1 \end{align}$$

$$\begin{align}0 \leqq &x \leqq \pi \\\\ 0 \leqq &\frac{7}{2}x \leqq \frac{7}{2}\pi \\\\ -1 \leqq &\cos \frac{7}{2}x \leqq 1 \end{align}$$

ここで④を満たすのは、
\( \ 0 \leqq \displaystyle\frac{1}{2}x \leqq \displaystyle\frac{ \pi }{ 2 } \ \)   すなわち、   \( \ 0 \leqq x \leqq \pi \ \)
かつ
\( \ 0 \leqq \displaystyle\frac{7}{2}x \leqq \displaystyle\frac{ \pi }{ 2 } \ \)   すなわち、   \( \ 0 \leqq x \leqq \displaystyle\frac{ \pi }{ 7 } \ \)
または、
\( \ \displaystyle\frac{3}{2}\pi \leqq \displaystyle\frac{7}{2}x \leqq \displaystyle\frac{5}{2}\pi \ \)   すなわち、   \( \ \displaystyle\frac{3}{7}\pi \leqq x \leqq \displaystyle\frac{5}{7}\pi \ \)  のとき。

整理して、
\( \ 0 \lt x \lt \displaystyle\frac{ \pi }{7} \ , \ \displaystyle\frac{3}{7}\pi \lt x \lt \displaystyle\frac{5}{7}\pi \ \) 

⑤については、\( \ 0 \leqq x \leqq \pi \ \) のとき、\( \ \sin \displaystyle\frac{1}{2}x \lt 0 \ \) は満たさないので、不適。

以上より、
\( \ 0 \lt x \lt \displaystyle\frac{ \pi }{ {\color{#0004fc}{7}} } \ , \ \displaystyle{\color{#0004fc}{\frac{3}{7}}}\pi \lt x \lt \displaystyle{\color{#0004fc}{\frac{5}{7}}}\pi \ \) 

Lukia

ページ冒頭に「加法定理」なんてあるので、一瞬戸惑うかもしれませんが、
\( \ \alpha \ \)と\( \ \beta \ \)の連立方程式を解けば、以降なんとか解けるようにしてありますね。
大学入試センター試験にしてもそうですが、
大学入学共通テストは、これまで学んできた、算数・数学の知識をフル活用させるつくりになっていますので、困ったら、簡単な表現にできないかを考えてみてください。

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2023年数学ⅡBの記事一覧

2023年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。