正十二面体とベクトル（その1）【大学入学共通テスト】
読了時間: 約1分1秒
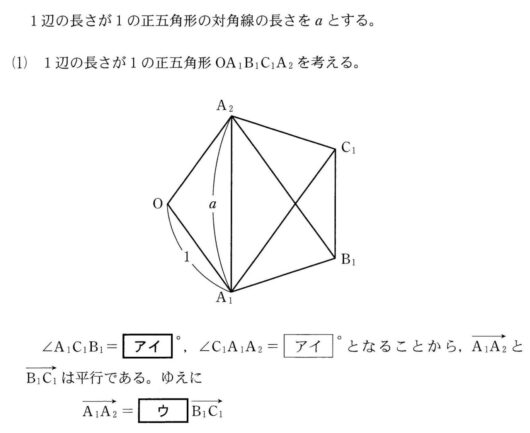
\( \ \triangle \mathrm{A_1B_1C_1} \ \)は、\( \ \mathrm{B_1A_1}=\mathrm{B_1C_1}=1 \ \)の二等辺三角形。
\( \ \angle \mathrm{A_1C_1B_1}=\angle \mathrm{C_1A_1B_1}=\theta \ \) とする。
\( \ n \ \)角形(ただし \( \ n \geqq 3 \ \))の外角の和は\( \ 360^{\circ} \ \)である。
\( \ \angle \mathrm{A_1C_1B_1}=\angle \mathrm{C_1A_1B_1}=\theta \ \) とする。
\( \ n \ \)角形(ただし \( \ n \geqq 3 \ \))の外角の和は\( \ 360^{\circ} \ \)である。
ゆえに、\( \ \angle \mathrm{A_1B_1C_1} \ \) の外角は
\( \ \displaystyle\frac{360}{5}=2\theta \ \)
\( \ \theta={\color{#0004fc}{36}}^{\circ} \ \)
辺\( \ \mathrm{A_1A_2} \ \)と辺\( \ \mathrm{B_1C_1} \ \) において、
\( \ \angle \mathrm{A_1C_1B_1}=\angle \mathrm{C_1A_1A_2} \ \)であるといえるので、
錯角が等しいことより、2辺は平行であるといえる。
ゆえに、\( \ \overrightarrow{\mathrm{A_1A_2}}={\color{#0004fc}{a}}\overrightarrow{\mathrm{B_1C_1}} \ \)
\( \ \angle \mathrm{A_1C_1B_1}=\angle \mathrm{C_1A_1A_2} \ \)であるといえるので、
錯角が等しいことより、2辺は平行であるといえる。
ゆえに、\( \ \overrightarrow{\mathrm{A_1A_2}}={\color{#0004fc}{a}}\overrightarrow{\mathrm{B_1C_1}} \ \)
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール
Author Profile
