高校数学の絶対値の問題は、グラフでイメージしよう。（その1）
[mathjax]
絶対値の定義を「拡張」する。
私が、中学校の数学で習った「絶対値の定義」は、
「0までの距離（0からの距離）」でした。
中学数学の間は、数直線上で考えるだけでしたので、これでよかったのですが、
$$\begin{align}今からは、&\ &\LARGE 「x軸との距離」\LARGE \ & と考えてもらえたらと思います。 \end{align}$$
問題
$$\Large \vert y \vert=8 を満たすyの値を求めよ。$$
$$そもそも、y=8が描けますか？$$
$$\begin{align}&まずは、y=8 をグラフに描いてみましょう。\\\\ &すると、以下のような赤い線になりますね。\ \end{align}$$
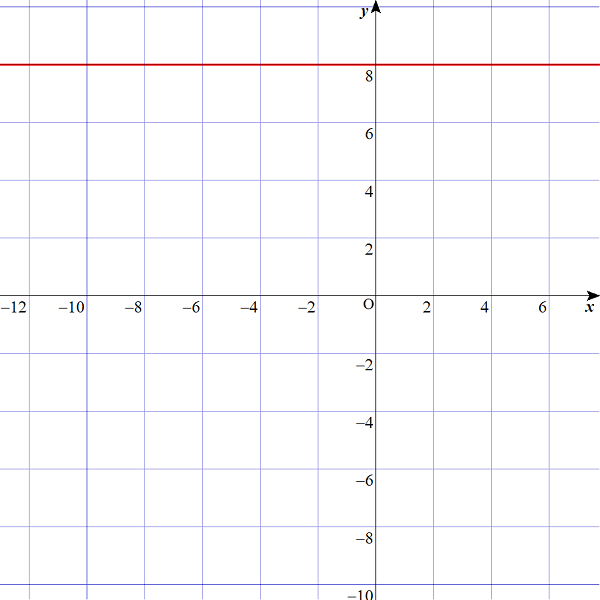
$$\begin{align}&ここで、「x軸との距離」も見てみましょう。\\\\ &当然ですが、距離は8ありますね。 \\\\ & \\\\ &では次に、y=-8 のグラフを描いてみましょう。\\\\ &すると、以下のような赤い線で表されます。 \end{align}$$
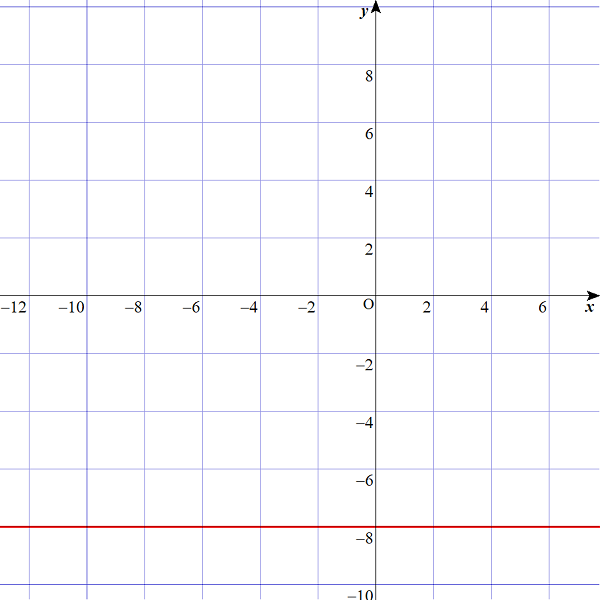
$$\begin{align}&これもまた、「x軸との距離」見てみると、\\\\ &y=8 のときと同様、距離は8であることがわかります。\end{align}$$
解答
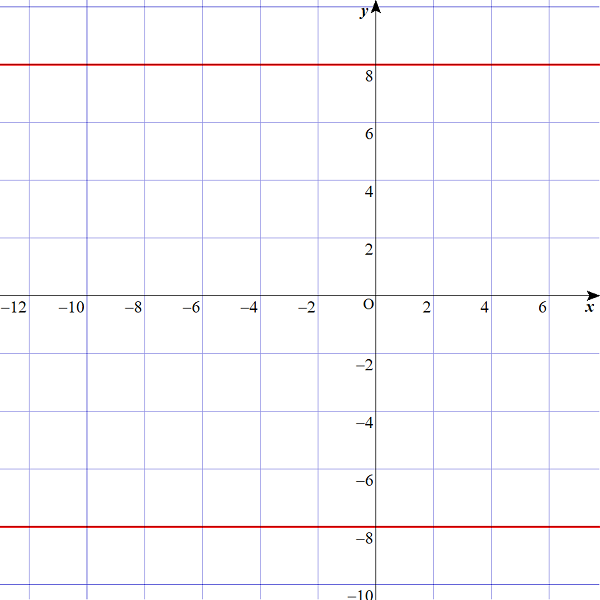
$$\begin{align}&ということは、問題の\vert y \vert=8 は、 \\\\ &「x軸との距離が8であるyの値は？」と聞かれていることになりますね。\\\\ &ゆえに、y= \pm 8 \left( y=8 , y=-8 でもよい\right) となります。\end{align}$$
絶対値をはずすなら、〇〇をつけろ？
ここで、あらためて式を見比べてみましょう。
$$\Large \begin{align}\vert y \vert&=8\\\\ y&= \pm 8\end{align}$$
左辺の絶対値の記号がはずれ、右辺に±（プラスマイナス）がついていますね。
なるほど～！絶対値をはずしたら、反対の辺に±の記号をつければいいんだ～！と思いたくなりますが、
実際には、もうひと手間かけてほしいところです。
「ひと手間」かけてみる。
絶対値をはずしたことで、最終的には右辺に±（プラスマイナス）がつくのですが、
もともとは、左辺についた±（プラスマイナス）を右辺に移項したものだったのです。
$$\Large \begin{align}\vert y \vert&=8\cdots①\\\\ \pm y&=8 \cdots②\\\\ y&= \pm 8 \cdots③\end{align}$$
しばらくは、「ひと手間」かけてね♪
絶対値に関する問題をいっぱいこなして、解法の手順を習得できれば、
試験会場で、①から③に変換することは問題ありません。
むしろ、一気に変換できるようでないと、時間が足りなくなります。
（試験中、ちょっとずつモタモタすることは、致命的です。）
しかし、この記事を読んでくださる間は、おそらく、絶対値の問題を解くのに、いまひとつ自信が持てない。という段階であろうと思います。
しばらくは、このひと手間をかけて、式がグラフ化（イメージ化）できるようにしてください。
共有:
プロフィール
