絶対値の問題は、グラフがイメージできればずいぶん楽になる。
$$\Large xの方程式、\vert \vert x-1 \vert +3\vert =2x を解け。$$
絶対値の定義を思い出そう。
私が中学校の数学で習った「絶対値」の定義は、
「0までの距離」でした。
今回は、難しい説明は はしょってしまいますが、
距離に0はあるけど、マイナスはないですよね。
マイナスは「向き」を表すもので、移動する瞬間瞬間に存在している地点の集合を示す「距離」とは異なるものです。
つまり、向きはあちこちあっていいけど、距離そのものは、0以上の実数でなければならない。ということですね。
$$y=\vert x-1 \vert を考える。$$
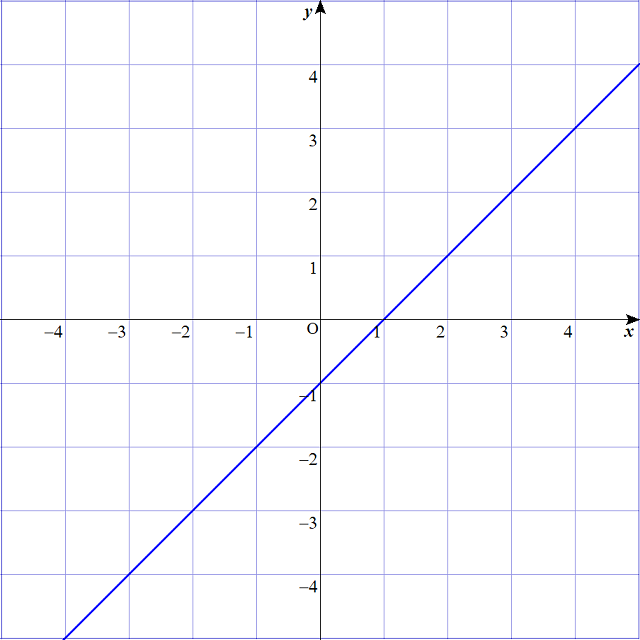
$$\Large y=x-1 のグラフは以下の通りです。$$
Lukia
とにかく実数であれば、
\(y\)の値も正や負、ときには0などのとにかく実数値を取るよ。ということが表されています。
$$\Large では、このyの絶対値はどうなるでしょうか。$$
Lukia
「距離」なのに、\(-2\)とか、\(-5\)っておかしくありませんか？
Lukia
\(x軸よりも下にある青い線は、「距離」を表すには不適切。\)
ということになりますね。
$$では、1 \leq x は表せないの？$$
「距離」を表すグラフとしては、今のままでは使えません。
しかし、先ほど「マイナス」は「向き」を示すもの。と述べました。
ということは、例えば「-1」は、
$$y軸の正の向き（グラフ中の矢印）に対して逆向きの距離1の位置にある。$$
と言い換えられますね。
$$つまり、y=\vert x-1 \vert のグラフを描きたいなら、$$
$$y=x-1 のグラフを描いて、x軸で折り返せばよいのです。$$
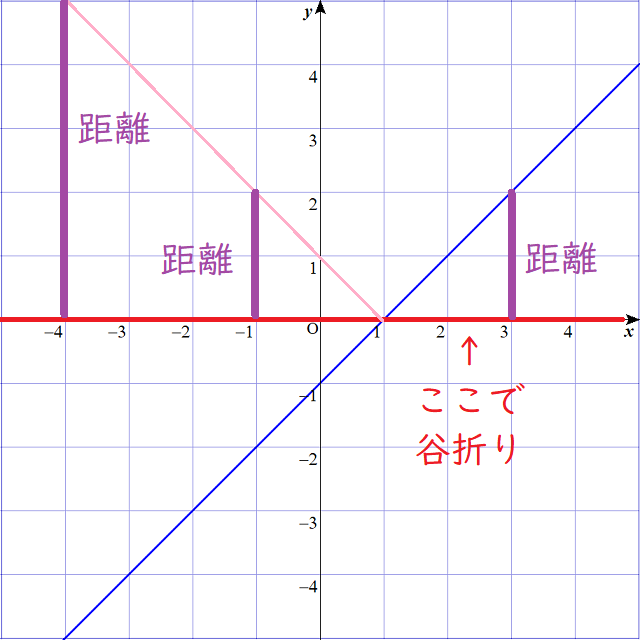
Lukia
すると、赤い線よりも下にあった青い線は、ピンクの線に移り変わります。
つまり、\(1 \leq x\)では、\(y=-x+1\)となるのです。
Lukia
Lukia
青い線とピンクの線によってあらわされることになります。
$$\begin{align}すなわち y&=\vert x-1 \vert は、\\\\ y&=x-1 \left( 1\leq x のとき\right) \cdots ①\\\\ y&=-x+1 \left( x \lt 1 のとき\right) \cdots ②であるといえます。\end{align}$$
以下は、これを用いて解いていきます。
$$① 1 \leq x のとき$$
$$\begin{align}左辺&=\vert x-1+3 \vert \\\\ &=\vert x+2 \vert\end{align}$$
$$\begin{align}y&=\vert x+2 \vert は、以下のグラフの青い実線・点線で表される。\\\\ &ただし、1 \leq xより、\\\\ &グラフとして存在するのは青い実線のみ。\\\\ &青い実線は、y=x+2 , \left( 1 \leq x\right) である。 \end{align}$$
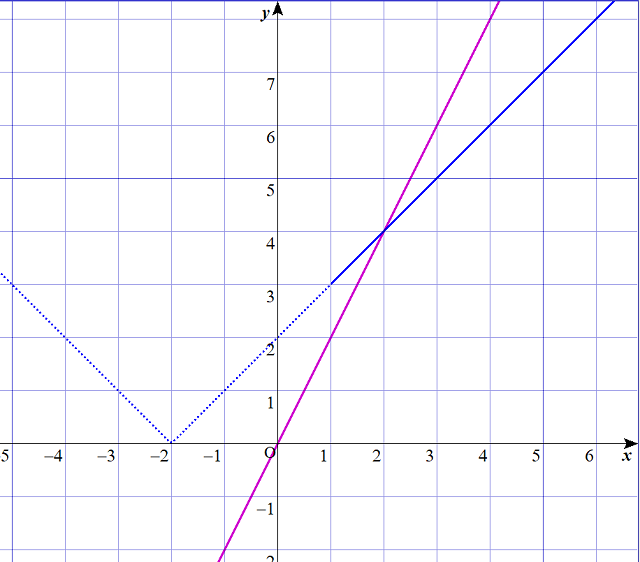
$$\Large x+2=2x , \left( 1 \leq x\right) を解く。$$
$$\Large x=2 \cdots ①$$
$$② x \lt 1 のとき$$
$$\begin{align}左辺&= \vert -x+1+3 \vert\\\\ &=\vert -x+4 \vert \\\\ &すなわち、y=\vert -x+4 \vert は、以下のグラフの赤い実線・点線で示される。\\\\ &ただし、x \lt 1 より、\\\\ &グラフとして存在するのは赤い実線のみ。 \\\\ &赤い実線は、y=-x+4 , \left( x \lt 1\right) である。 \end{align}$$
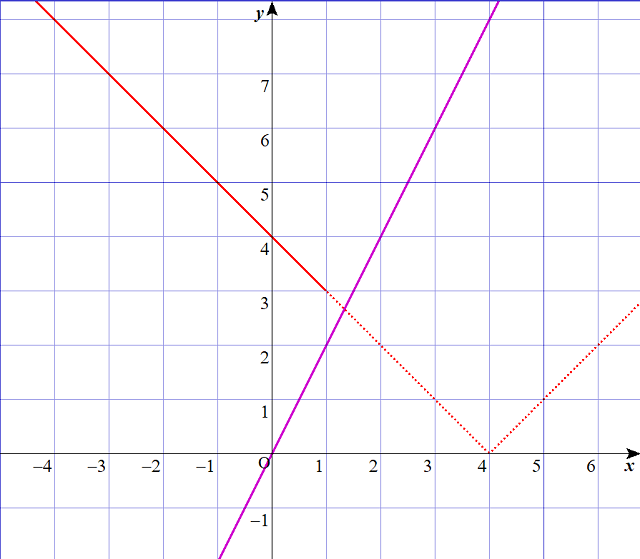
$$\Large \begin{align}&-x+4=2x , \left( x \lt 1\right) を解く。 \\\\ x&=\frac{4}{3} \\\\ &しかし、x \lt 1 より不適。\cdots ②\end{align}$$
$$\Large ① , ②より、x=2$$
Lukia
以前、Yahoo!知恵袋で回答した際に、学校では、このようにグラフからのアプローチを教わらないと質問者さんが言っていました。
絶対値の問題は、数式の状態で考えると相当しんどいです。
基本的には、絶対値を外した状態のグラフを描いておいて、
後から\(x\)軸でパタンと折り返せばよいだけですので、いくつか類似問題をやってマスターすることをオススメします。
共有:
プロフィール
