高校数学の絶対値の問題は、グラフでイメージしよう。(その7)

[mathjax]
自宅のパソコンでブログ記事を書いていたはずが、
突然不思議な世界に迷い込み、
高校生?恐竜、ディノさんと出会ってしまった私。
ディノさんは、絶対値の問題の解き方を教えてくれたら、ひらけた場所までの案内をしてくれると言いますが・・・
さて、今日の問題の「解法」で、ディノさんは私を「解放」してくれるのでしょうか。
![]()

ディナ
ほらっ、先生も朝だよッ!

Lukia
目を開けると・・・
そこには、大きな恐竜の顔が!

Lukia
・・・
あっ、そうだ、ここディノさんちだ。
あっ、お母さん、おはようございます。

ディナ
昨夜は悪かったねぇ。
息子の勉強につき合わせちゃったうえ、私にもつきあってもらっちゃって~。
「女子会」っていうの~?
た~のしかったぁ~。

Lukia

ディナ
いっぱい食べて、今日もがんばっておくれよッ。
突如現れた「ディナさん」は、ディノさんのお母さんです。
有無を言わせない強烈なキャラクターの持ち主で、さすがのディノさんもこのお母さんのペースは崩せないようです。


ディナ

Lukia

ディナ

ディノ

ディナ
じゃ、さっさとお勉強始めるんだよ。
先生が、朝からついててくれてるなんて、これはチャンスだよ!
ディノさんは、私のほうを向いて、こっそりと言いました。

ディノ

Lukia
ま、まだ問題もあるようですし、もう一問、お付き合いします。

ディノ
問題
$$\Large \color{blue}{2\vert x \vert}+\color{red}{\vert 2x+3 \vert}=7$$
簡単な図を描こう。
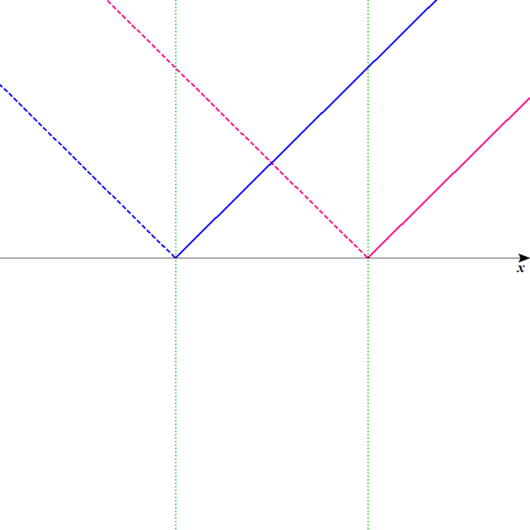

Lukia

ディノ

Lukia

ディノ

Lukia
ま、でも、やることは今までとそんなに変わりませんよ。
大丈夫です。
範囲を設定しよう。

Lukia
\(\color{blue}{2\vert x \vert=0}\)となるときを探しますが、
両辺を2で割ったらどうなりますか?

ディノ
右辺は0だから・・・
0のままだな!

Lukia
ですから、\(\color{blue}{2\vert x \vert=0}\)となるのは、
\(x=\color{blue}{0}\)のときといってよいですね。

ディノ
今まで通り、まずは絶対値記号に囲まれた部分から考えていけばいいんだな。

Lukia
ちなみに、赤いほうは問題ないですよね?

ディノ
\(\color{red}{\vert 2x+3 \vert=0}\)となるのは、
\(x=\color{red}{-\frac{3}{2}}\)のときだな。

Lukia
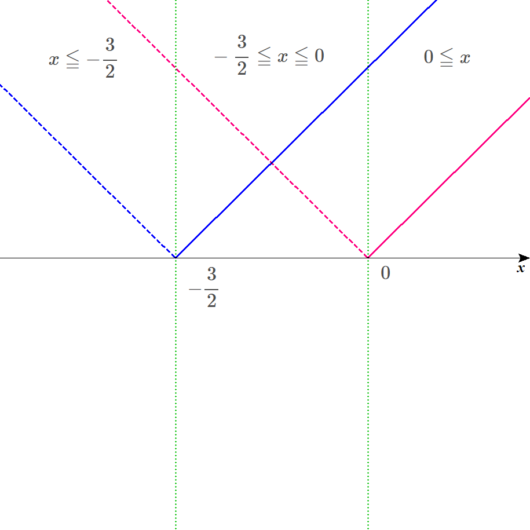
範囲ごとに式を書き込んでいく。

Lukia
青い式のほうは、少していねいな式変形を示します。
それをヒントに、式を書き込んでみてください。
\(\color{blue}{y=2\vert x \vert}\)
\(\color{blue}{y=2\left( \pm x\right)}\)
\(\color{blue}{y= \pm 2x}\)

ディノ
絶対値をていねいにはずして考えればいいわけだな。
ということは、
\(\color{blue}{y=2\vert x \vert}\)は、
\(y=\color{blue}{-2x}\) \(\left( \color{blue}{x \leq 0} のとき\right)\)
\(y=\color{blue}{2x}\) \(\left( \color{blue}{0 \leq x} のとき\right)\)
だな。

Lukia
徐々にはずすように。と教わったと思いますが、
絶対値も同じように考えてよいと思います。
では、ディノさん、
赤いほうもお願いしますね。

ディノ
\(\color{red}{y=\vert 2x+3 \vert}\)は、
\(y=\color{red}{-2x-3}\) \(\left( \color{red}{x \leq -\frac{3}{2}} のとき\right)\)
\(y=\color{red}{2x+3}\) \(\left( \color{red}{-\frac{3}{2} \leq x} のとき\right)\)
となる。

Lukia
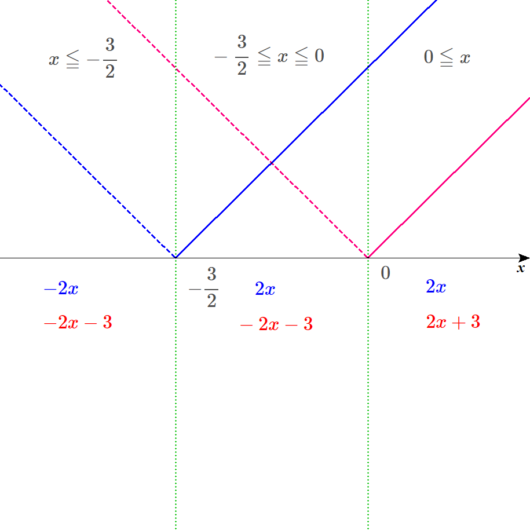
筆算する。

ディノ
今回も、二つの絶対値は+(プラス)でつながっているから、
たし算の筆算をすればいいよな。
というわけで、
左が、\(-4x-3\)
真ん中が、\(-3\)
右が \(4x+3\)になるぞ。

Lukia
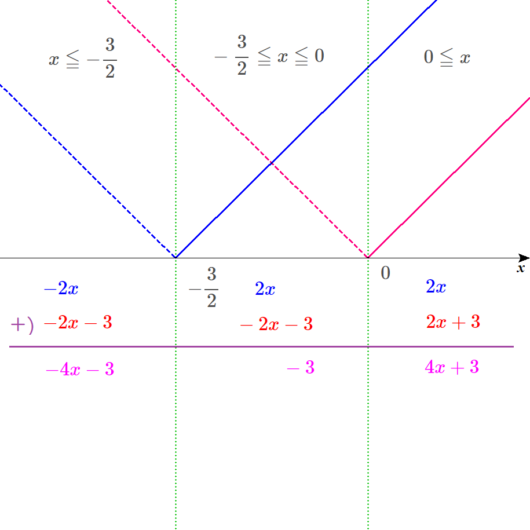
グラフを描くとこうなる。

Lukia
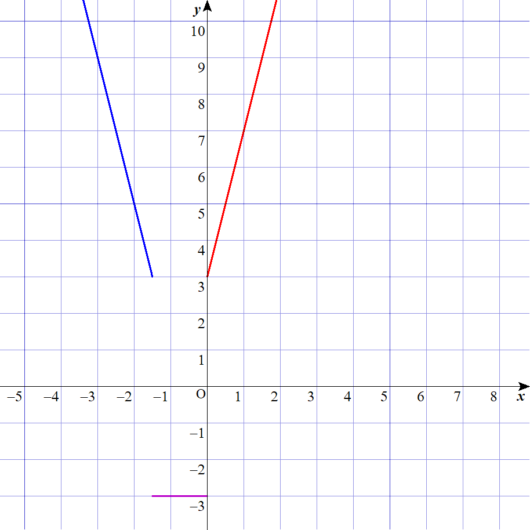
方程式を解く。

Lukia
いよいよ、=7 をつけて、方程式を解いてみましょう。

ディノ
\(x=-\frac{5}{2}\)だ。

ディノ

ディノ
\(x=1\) だな。
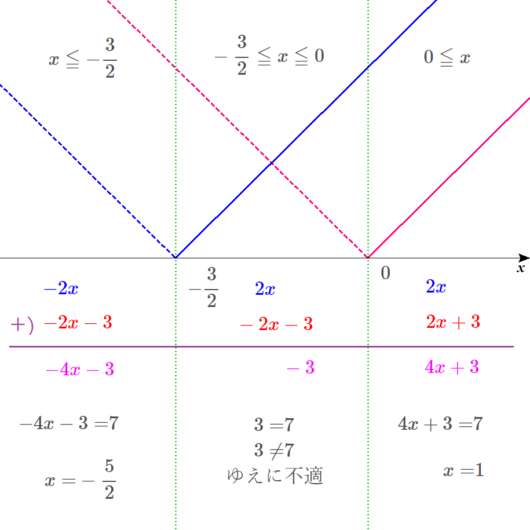

Lukia
真ん中の式は、3ではなくて、-3ですね。
正しくは、
\(-3=7\)
\(-3 \neq 7\)
となります。以下の図も同様です。
範囲を比較して答えを出す。

Lukia
左の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
真ん中の範囲の解ですが、今回はそもそも方程式が成り立たなかったので、解なし。であり、紫の矢印は示せません。
右の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。
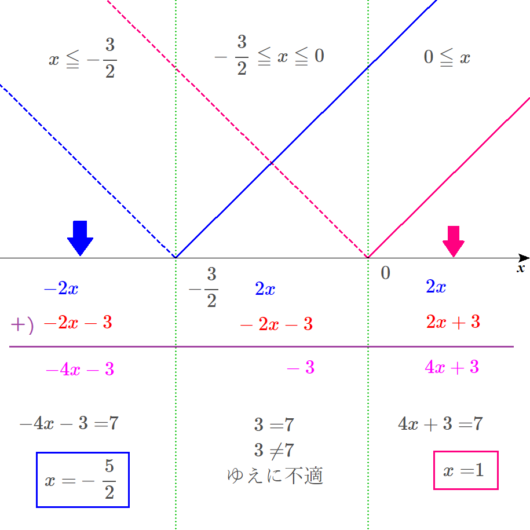

Lukia
青と赤の矢印はどうですか?

ディノ
ということは、この二つが解ということでいいな。
こたえ
$$\Large 2\vert x \vert+\vert 2x+3 \vert=7$$
$$\Large x=-\frac{5}{2} , x=1$$


Lukia
紫の線は、\(y=-3\)ですから、どうひっくりかえっても、\(y=7\)とは交われませんね。

ディノ
目に見える形になると、答えにも自信が持てるもんだな。
今回こそ「解放」なるか?

Lukia
よかったよかった。
では、ディノさん、ホントにそろそろ「ひらけた場所」に案内してくださいよぉ。

ディノ
あ、ああ、そうだなぁ。
いっぱい教えてもらったしな。
じゃ、案内し・・・

ディナ

ディノ

ディナ

Lukia

ディナ
ほら、今日はバーベキューパーティーだから、いっぱい食べてッ!


Lukia

ディナ
楽しいわよぉ~~~!

Lukia

ディナ
バーベキュー食べきるまで、帰さないわよ~。
ご近所にも知らせちゃったんだから、いてくれなきゃ困るわよ~。


Lukia

ディノ

ディナ
午後からも頭をはたらかせるには、まずはガッツリお肉食べなきゃね♪
どこの世界も、お母さんが最強のようです。(^◇^;)
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません