高校数学の「三角形と余弦定理」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約1分59秒
[mathjax]
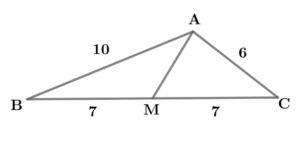三角形\( \ \mathrm{ABC} \ \)において、辺\( \ \mathrm{AB} \ \)の長さが\( \ 10 \ \),
辺\( \ \mathrm{BC} \ \)の長さが\( \ 14 \ \),
辺\( \ \mathrm{CA} \ \)の長さが\( \ 6 \ \)で、
辺\( \ \mathrm{BC} \ \)の中点を\( \ \mathrm{M} \ \)とする。
このとき、辺\( \ \mathrm{AM} \ \)の長さを求めよ。
Lukia
余弦定理を用いて解いていくのですが、
ここでポイントになるのが、三角形におけるひとつの内角と隣り合う外角との関係です。
ここでポイントになるのが、三角形におけるひとつの内角と隣り合う外角との関係です。
\( \ \triangle \mathrm{ABM} \ \)において、\( \ \angle \mathrm{AMB}=\theta \ \)とする。
余弦定理より
\( \ \cos \theta=\frac{\mathrm{AM}^2+7^2-10^2}{2\cdot 7\cdot \mathrm{AM}} \ \)
余弦定理より
\( \ \cos \theta=\frac{\mathrm{AM}^2+7^2-10^2}{2\cdot 7\cdot \mathrm{AM}} \ \)
\( \ \triangle \mathrm{AMC} \ \)において、余弦定理より
\( \ \cos \angle \mathrm{AMC}=\frac{\mathrm{AM}^2+7^2-6^2}{2\cdot \mathrm{AM}\cdot 7} \ \)
ここで、\( \ \angle \mathrm{AMB}+\angle \mathrm{AMC}=180^{\circ} \ \)より
\( \ \angle \mathrm{AMC}=180^{\circ}-\theta \ \)であるから、
\( \ \cos \angle \mathrm{AMC}=-\cos \theta \ \)である。
\( \ \cos \theta=\frac{\mathrm{AM}^2+7^2-10^2}{2\cdot 7\cdot \mathrm{AM}}=-\frac{\mathrm{AM}^2+7^2-6^2}{2\cdot \mathrm{AM}\cdot 7} \ \)
\( \ 2\mathrm{AM}^2+2\cdot 49-100-36=0 \ \)
\( \ \mathrm{AM}^2=19 \ \)
\( \ \mathrm{AM}= \pm \sqrt{19} \ \)
\( \ \mathrm{AM} \gt 0 \ \)より
\( \ \mathrm{AM}=\sqrt{19} \ \)
Lukia
上記のやり方をまとめると、以下のような公式のようなものが導けます。
しかし、2021年以降、これが通用する場面は少ないかも。
記述形式の問題が増えるので、公式を暗記するだけの勉強方法では太刀打ちできません。
数検の一次である計算技能検定だったら、答えを書けばいいだけなので、その場合なら役立つかもしれませんが、まぁ、暗記するよりかは、計算の速さや確実さを増すような訓練をするほうがよっぽど実践的でしょうね。
しかし、2021年以降、これが通用する場面は少ないかも。
記述形式の問題が増えるので、公式を暗記するだけの勉強方法では太刀打ちできません。
数検の一次である計算技能検定だったら、答えを書けばいいだけなので、その場合なら役立つかもしれませんが、まぁ、暗記するよりかは、計算の速さや確実さを増すような訓練をするほうがよっぽど実践的でしょうね。
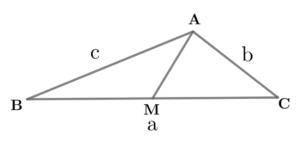
\( \ \mathrm{AM}^2=\frac{2c^2+2b^2-a^2}{4} \ \)
共有:
プロフィール
Author Profile