高校数学の「箱ひげ図からデータを推定する」問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約2分14秒
[mathjax]
問題
次のデータは,\( \ 20 \ \)点満点のテストを受けた7人の得点である。
\( \ 9 \ , \ 15 \ , \ 12 \ , \ 7 \ , \ 11 \ , \ a \ , \ b \ \) （単位は点）
ただし, \( \ a \ , \ b \ \)は\( \ 0 \leq a \leq b \leq 20 \ \)を満たすものとする。
平均値が\( \ 11 \ \)点, 四分位範囲が\( \ 4 \ \)点であるとき,
\( \ a \ , \ b \ \)の値をそれぞれ求めよ。
\( \ 9 \ , \ 15 \ , \ 12 \ , \ 7 \ , \ 11 \ , \ a \ , \ b \ \) （単位は点）
ただし, \( \ a \ , \ b \ \)は\( \ 0 \leq a \leq b \leq 20 \ \)を満たすものとする。
平均値が\( \ 11 \ \)点, 四分位範囲が\( \ 4 \ \)点であるとき,
\( \ a \ , \ b \ \)の値をそれぞれ求めよ。
箱ひげ図を描くつもりで、点数順に並べてみる。
Lukia
四分位範囲とありますから、箱ひげ図を描くつもりで考えていきましょう。
\( \ {7} \equiv {3} \pmod {4} \ \) より,
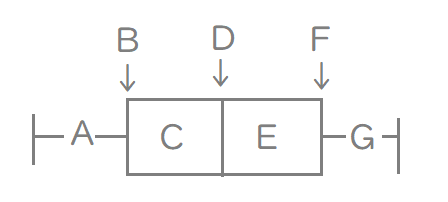
描かれる箱ひげ図は以下の図のようになります。
点数の少ない順にA～Gの7人を並べたとすると、
第1四分位数にB
第2四分位数にD
第3四分位数にF が該当することになります。
\( \ {7} \equiv {3} \pmod {4} \ \) より,
描かれる箱ひげ図は以下の図のようになります。
点数の少ない順にA～Gの7人を並べたとすると、
第1四分位数にB
第2四分位数にD
第3四分位数にF が該当することになります。
Lukia
7人の平均値が11点ということですから、
\( \ 9+15+12+7+11+a+b=77 \ \)
これを解いて、
\( \ a+b=23 \ \)が成り立つことになります。
\( \ 9+15+12+7+11+a+b=77 \ \)
これを解いて、
\( \ a+b=23 \ \)が成り立つことになります。
Lukia
ひとまず\( \ a \ \)点と\( \ b \ \)点を除いた5人分の点数を低い順に並べると、
\( \ 7 \ , \ 9 \ , \ 11 \ , \ 12 \ , \ 15 \ \) となります。
\( \ 7 \ , \ 9 \ , \ 11 \ , \ 12 \ , \ 15 \ \) となります。
Lukia
四分位範囲が\( \ 4 \ \)という条件を考えてみましょう。
生徒Fと生徒Bの点数差が4点ということになります。
ここで、生徒Bの点数を\( \ x \ \)とすると,
生徒Fの点数は,\( \ x+4 \ \)と表せますね。
生徒Fと生徒Bの点数差が4点ということになります。
ここで、生徒Bの点数を\( \ x \ \)とすると,
生徒Fの点数は,\( \ x+4 \ \)と表せますね。
Lukia
さらに、生徒Bと生徒Fの間には、
生徒C, 生徒D, 生徒Eが並んでいます。
生徒Dの点数が第2四分位数となるには、この3人が1点差で並ぶ必要がありますね。
生徒C, 生徒D, 生徒Eが並んでいます。
生徒Dの点数が第2四分位数となるには、この3人が1点差で並ぶ必要がありますね。
Lukia
ここで、生徒B、すなわち第1四分位数が\( \ 9 \ \)と仮定してみましょう。
すると,生徒Cは\( \ 9+1=10 \ \)
生徒Dは\( \ 10+1=11 \ \)
生徒Eは\( \ 11+1=12 \ \)
生徒Fは\( \ 12+1=13 \ \) と考えられます。
すると、生徒Aが\( \ 7 \ \)点、
生徒Gが\( \ 15 \ \)点となり、すべての点数があてはまったことになります。
さらに、\( \ a=10 \ , \ b=13 \ \)となるので、\( \ a+b=23 \ \)も満たしていますね。
すると,生徒Cは\( \ 9+1=10 \ \)
生徒Dは\( \ 10+1=11 \ \)
生徒Eは\( \ 11+1=12 \ \)
生徒Fは\( \ 12+1=13 \ \) と考えられます。
すると、生徒Aが\( \ 7 \ \)点、
生徒Gが\( \ 15 \ \)点となり、すべての点数があてはまったことになります。
さらに、\( \ a=10 \ , \ b=13 \ \)となるので、\( \ a+b=23 \ \)も満たしていますね。
Lukia
今回は、たまたま生徒Bの点数を9と仮定して、たまたまうまくいったのですが、
7と仮定する人や、11と仮定する人もいるかもしれませんね。
その場合は、必ずどこかに矛盾点が表れるので、いくつかの仮定を試すうち正解にたどり着けると思いますが、
「最低点（生徒A）を7点として・・・」と、直感的にやってみると、うまくいくことが多いです。
この仮定は、点数順に並べておかないと設定できません。
どうしたらいいかわからない場合は、並べ替えてやるところからでもやってみましょう。
7と仮定する人や、11と仮定する人もいるかもしれませんね。
その場合は、必ずどこかに矛盾点が表れるので、いくつかの仮定を試すうち正解にたどり着けると思いますが、
「最低点（生徒A）を7点として・・・」と、直感的にやってみると、うまくいくことが多いです。
この仮定は、点数順に並べておかないと設定できません。
どうしたらいいかわからない場合は、並べ替えてやるところからでもやってみましょう。
こたえ
$$a=10\quad ,\quad b=13$$
共有:
プロフィール
Author Profile
