中学数学の「図形と計量」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約1分41秒
[mathjax]
問題
以下の図形において、
辺\( \ \mathrm{AB} \ \)の長さが\( \ 21 \ \),辺\( \ \mathrm{BC} \ \)の長さが\( \ 8 \ \),辺\( \ \mathrm{AC} \ \)の長さが\( \ 15 \ \),
\( \ \angle \mathrm{CAD}=\angle \mathrm{DAE} \ \)を満たすとき,辺\( \ \mathrm{CD} \ \)の長さを求めよ。
辺\( \ \mathrm{AB} \ \)の長さが\( \ 21 \ \),辺\( \ \mathrm{BC} \ \)の長さが\( \ 8 \ \),辺\( \ \mathrm{AC} \ \)の長さが\( \ 15 \ \),
\( \ \angle \mathrm{CAD}=\angle \mathrm{DAE} \ \)を満たすとき,辺\( \ \mathrm{CD} \ \)の長さを求めよ。
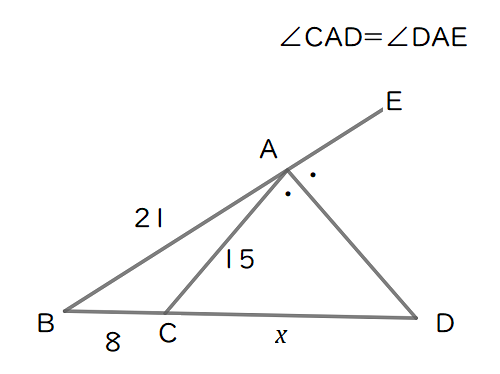
補助線に助けてもらおう。
Lukia
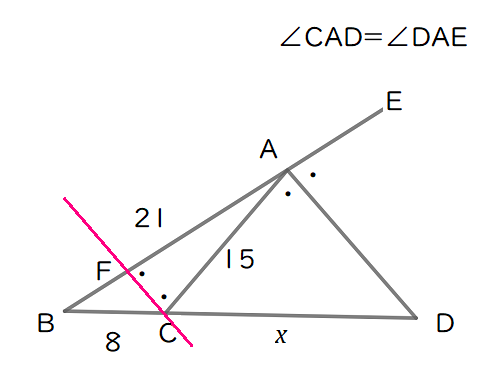
点\( \ \mathrm{C} \ \)を通り,線分\( \ \mathrm{AD} \ \)に平行な直線を引く。
その直線と辺\( \ \mathrm{AB} \ \)との交点を\( \ \mathrm{F} \ \)とする。
その直線と辺\( \ \mathrm{AB} \ \)との交点を\( \ \mathrm{F} \ \)とする。
平行線の錯角により,\( \ \angle \mathrm{DAC}=\angle \mathrm{ACF}\quad \cdots\quad ① \ \)
同位角より,\( \ \angle \mathrm{EAD}=\angle \mathrm{AFC}\quad \cdots\quad ② \ \)
ゆえに,\( \ \triangle \mathrm{AFC} \ \)は\( \ \mathrm{AF}=\mathrm{AC} \ \)の二等辺三角形である。
\( \ \mathrm{AC}=15 \ \)より\( \ \mathrm{AF}=15 \ \),\( \ \mathrm{FB}=6 \ \)である。
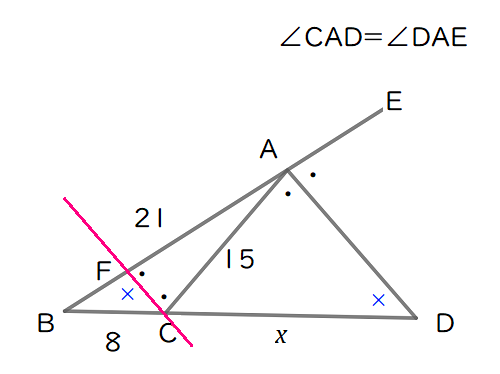
相似比から辺の長さを求める。
Lukia
\( \ \triangle \mathrm{BCF} \ \)と\( \ \triangle \mathrm{BDA} \ \)において,
\( \ \angle \mathrm{CBF}=\angle \mathrm{DBA}\quad \cdots\quad ① \ \)
同位角より,\( \ \angle \mathrm{BCF}=\angle \mathrm{BDA}\quad \cdots\quad ② \ \)
①と②より,\( \ \triangle \mathrm{BCF} \sim \triangle \mathrm{BDA} \ \)である。
\( \ \angle \mathrm{CBF}=\angle \mathrm{DBA}\quad \cdots\quad ① \ \)
同位角より,\( \ \angle \mathrm{BCF}=\angle \mathrm{BDA}\quad \cdots\quad ② \ \)
①と②より,\( \ \triangle \mathrm{BCF} \sim \triangle \mathrm{BDA} \ \)である。
Lukia
\( \ \mathrm{BF}:\mathrm{FA}=\mathrm{BC}:\mathrm{CD} \ \)
\( \ 6:15=8:x \ \)
\( \ x=20 \ \)
\( \ 6:15=8:x \ \)
\( \ x=20 \ \)
こたえ
$$x=20$$
共有:
プロフィール
Author Profile
