高校数学の「集合と論理(xの値の範囲）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月2日2023年1月14日集合と論理実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

まずは情報を視覚化しよう。（読み飛ばしOK)

Lukia

「何からはじめたらいいかわからないときは、何から手をつけても同じ。」
なんていいますが、まさにその通り。
やる気スイッチは、脳の側坐核そくざかくという場所にあるので、某塾のCMのように背中やおでこみたいな触りやすい位置にはないんですね。
他人は簡単に触れられませんが、自分の体なら、自分でなんとかできます。
手を動かすことで、なんとなくアイディアが浮かんだり、やる気が出てきたりしますので、まずはペンを持つことが大切です。

Lukia

また、数学の場合、多くは「文字情報を視覚化」することで、解法の糸口がつかめることが多いです。問題文に書かれている情報を、図形や数直線、グラフなどに置き換えることで、わかっていること、まだわからない（答えとなる）こと、自分が知っていること、知らないことなどが明確になってきます。

Lukia

では、まずは「確実にわかっている」集合\( \ \mathrm{A} \ \)と集合\( \ \mathrm{B} \ \)を数直線で表してみましょう。

Lukia

集合\( \ \mathrm{C} \ \)には\( \ x \ \)どころか、定数\( \ k \ \)が含まれていますので、逆に安易に数直線にしてしまうのは危険です。
視覚化することは、解法の糸口をつかむのに有効な手段ですが、描くときには、「仮だよ。仮。」と思っていても、
描かれてしまうと、「仮」ということをすっかり忘れてしまい、そのイメージに支配されてしまうおそれもあります。
仮と思って、\( \ k \ \)を\( \ 3 \ \)とおき、数直線を描くと、もう修正が利かなくなります。
なんでもかんでも、視覚化すればいいのではなく、「確実にわかっていること」を視覚化するようにしましょう。

集合AとBを視覚化する。

$$\begin{align}集合 \ \mathrm{B} \ &\vert x \vert \lt 3 \ &-3 \lt x \lt 3 \end{align}$$

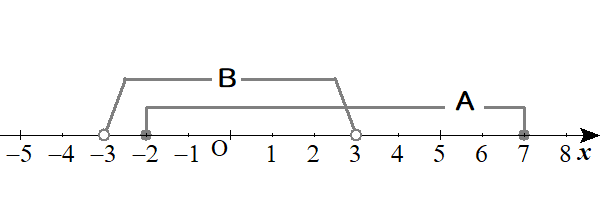
「または」より「かつ」の方が楽。

Lukia

集合を考えるとき、「ベン図」を使いますね。
私は、「ベン図」の「ベン」は、漢字で書くと難しすぎるから、あえてカタカナ表記にしているのかな。と思っていたのですが、
どうやら数学者のベンさんが考えた図だから、「ベン図」なんだそうです。
人の名前だというのを知ったのは、再受験生になってからなので、何歳になっても知らないことはあるもんだなぁ。と感心した記憶があります。

Lukia

大学入試センター試験でも、集合と論理の問題がよく出ますが、
「または」があったら、できるだけ「かつ」に直すことをオススメします。
ひと手間かかりますが、「かつ」に直すことで考える範囲が限定されるからです。

Lukia

たとえば下のような集合を考えるとします。

Lukia

\( \ \mathrm{A}\cup\mathrm{B} \ \)（A または　B）だったら、
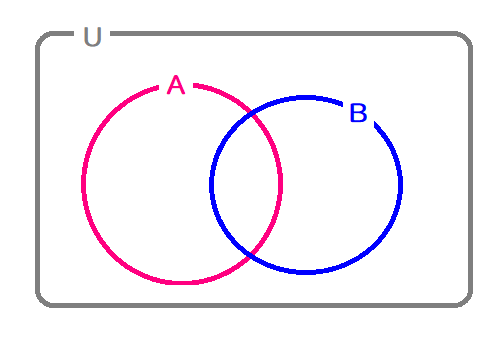
下の図でピンクに塗りつぶされた部分に含まれる要素を考えなければなりません。
全体集合 U を「日本人」とし、集合 A を「女性」、集合 B を「5人以上のアイドルグループ」とすると、
A または Bの要素に含まれるのは、ひとまず「日本人」であれば、「女性」でもいいし（だから、私Lukiaも含まれます。）
「5人以上のアイドルグループ」でもいいのですから、「嵐」でもいいし、「AKB48」でもいいし、過去にさかのぼって「6人だったころのももクロ」とかもいいことになってしまいます。
属性がひとつでもあてはまれば集合の要素となるので、「または」でつながれた集合の要素をもれなく数え上げるというのはとても難しいんですね。

Lukia

しかし、\( \ \mathrm{A}\cap\mathrm{B} \ \)（A かつ B)だと、
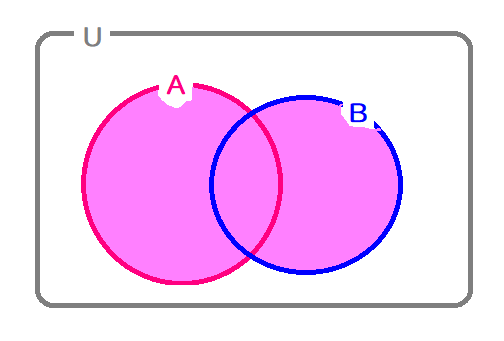
下の図のように、塗りつぶす部分が小さくなります。
「女性　かつ　5人以上のアイドルグループ」となると、私は「女性」ですがアイドルグループには属していないので省かれます。
「松田聖子」は「女性」ですし、「アイドル」でしたが、「5人以上のアイドルグループ」には属していなかったので、省かれます。
「嵐」はたしかに「5人以上のアイドルグループ」ですが、「女性」ではないので省かれます。
よって、「AKB48」や「過去のももクロ」などに限定されますね。

Lukia

前置きが長くなりましたが、「または」は要素をもれなく数え上げるのが難しいので、直せるもんなら「かつ」に直して考える。というのが、なんとなくでも理解していただければ幸いです。

集合と補集合、より狭いほうで考えよう。

Lukia

上の図のような集合を考えます。
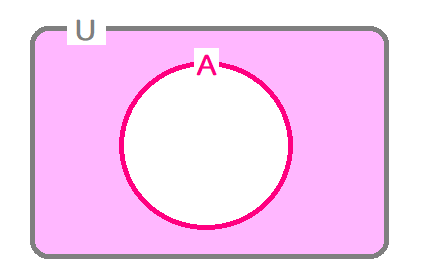
全体集合 \( \ \mathrm{U} \ \) は、「男女共学クラス」とします。
そして集合 \( \ \mathrm{A} \ \)　の属性は「女性」とします。
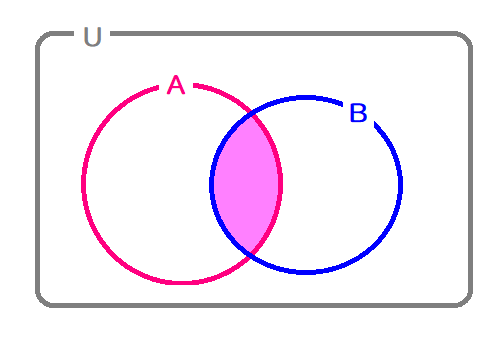
淡いピンクで塗りつぶされた部分を「補集合ほしゅうごう」といい、\( \ \overline{A} \ \)で表します。
クラスの「男子」は、この補集合に属することになりますね。

Lukia

集合と補集合は、共通する要素がないので、
たとえば、集合が、「または」でつながっているため、属性や要素の数が多すぎて考えにくいとき、
逆の補集合を考えておいて、補集合をひっくり返せば、そもそもの集合を考えることになりますね。

Lukia

あらためて、\( \ \overline{A}\cup\mathrm{B} \ \)をベン図で表すと以下の薄紫で塗りつぶされた部分になります。
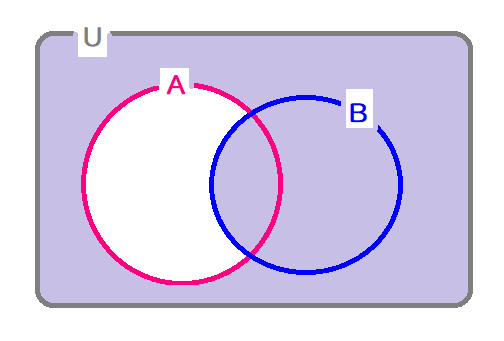
集合 B だけでなく、AでもBでもない部分まで考えなければならないので、相当大変そうですよね。
真っ白いままの集合Aの部分だけ考えられればなぁ・・・と思いませんか？（思ってほしい！）

Lukia

というわけで、\( \ \overline{A}\cup\mathrm{B} \ \)の補集合を考え、その後、補集合の「補集合」を考えることにします。

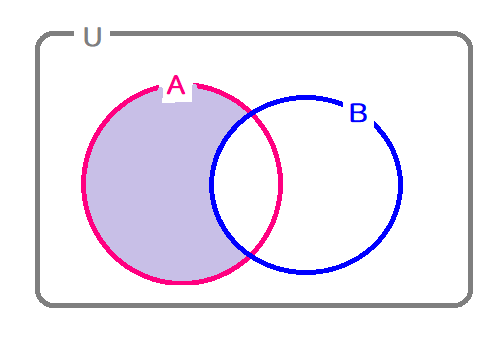
$$\begin{align}\overline{\overline{A}\cup\mathrm{B}}=&\overline{\overline{A}} \ \overline{\cup} \ \overline{B} \\\\ =&\mathrm{A}\cap\overline{B} \\\\ すなわち&-2 \leq x \leq 7 \ かつ \ x \leq -3 \ , \ 3 \leq x \\\\ すなわち\quad &3 \leq x \leq 7 \end{align}$$

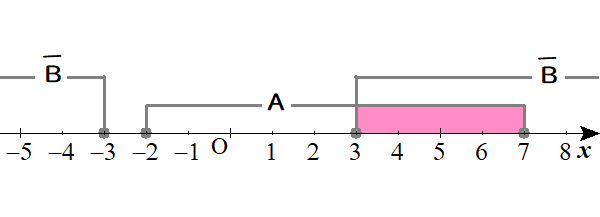
$$\begin{align}\overline{A}\cup\mathrm{B}=&\overline{\mathrm{A}\cap\overline{B}} \\\\ すなわち \ &\overline{3 \leq x \leq 7} \\\\ すなわち \ &x \lt \color{#0004fc}{3} \ , \ \color{#0004fc}{7} \lt x \end{align}$$

$$\mathrm{A}\cap\overline{B} \ は \ \color{#0004fc}{3} \leq x \leq \color{#0004fc}{7}$$

包含関係を理解しておこう。

 

実数全体を全体集合とし,その部分集合\( \ \mathrm{A \ , \ B \ , \ C} \ \)が
\( \ \mathrm{A}=\lbrace x \ | \ -2 \leq x \leq 7\rbrace \ \)
\( \ \mathrm{B}=\lbrace x \ | \ \vert x \vert \lt 3\rbrace \ \)
\( \ \mathrm{C}=\lbrace x \ | \ k-5 \leq x \leq k+7\rbrace \ \left( k \ は定数\right)\)　であるとする。
このとき,
\( \ \mathrm{B}\subset\mathrm{C} \ \)　のためには,\( \ -\color{#0004fc}{オ} \leq k \leq \color{#0004fc}{カ} \ \)　である。

Lukia

記事自体がだいぶん長く、ボリューミーになってきたので、なるべくコンパクトにしていきたいと思います。
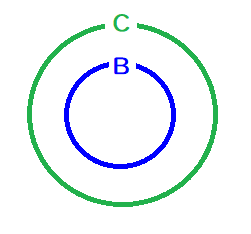
\( \ \mathrm{B}\subset\mathrm{C} \ \)をベン図で表すと以下のようになります。

Lukia

集合\( \ \mathrm{B} \ \)がすっぽりと集合\( \ \mathrm{C} \ \)の中におさまっている。という状態です。当然、もれなくです。
包含関係は、後々、命題の真偽を判断したり、必要条件・十分条件などを考えるときにも活かされます。
命題が真であることや、必要条件・十分条件は、一方の集合が、ひとつのもれなく、例外なく、他方の集合に含まれるときに成り立ちます。
というわけで、今回は、しっかりと集合\( \ \mathrm{B} \ \)を集合\( \ \mathrm{C} \ \)に内包させてやりましょう。

Lukia

上の図は、集合\( \ \mathrm{B} \ \)の範囲を数直線上に表しています。
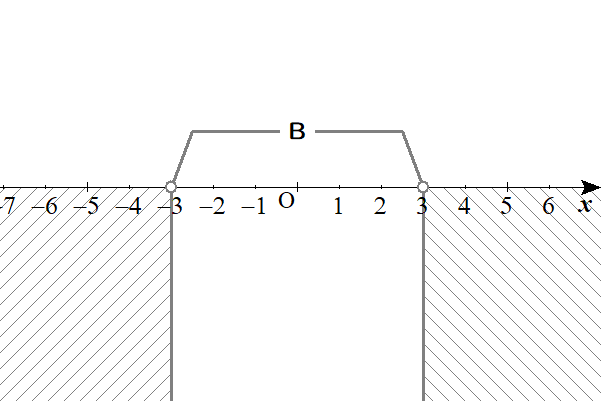
集合\( \ \mathrm{C} \ \)が集合\( \ \mathrm{B} \ \)をすっぽり内包してしまうには、集合\( \ \mathrm{C} \ \)の両端が、集合\( \ \mathrm{B} \ \)の両端の外側にある必要がありますね。
上の図の斜線部分に集合\( \ \mathrm{C} \ \)の両端があるときを考えればよいことになります。

$$\begin{align}\mathrm{B}\subset\mathrm{C} \ が&成り立つためには, \\\\ &k-5 \leq -3\quad かつ\quad 3 \leq k+7\quad である必要がある. \\\\ 整理して,&-\color{#0004fc}{4} \leq k \leq \color{#0004fc}{2} \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。