高校数学の「平面ベクトルの内分比の活用」に関する問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約9分8秒
問題
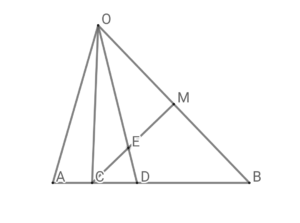
三角形\( \ \mathrm{OAB} \ \)があり、 \( \ \mathrm{OA}=3 \ \)、\( \ \mathrm{OB}=4 \ \)、\( \ \angle \mathrm{AOB}=60^{\circ} \ \) とする。
また、 辺\( \ \mathrm{OB} \ \)の中点を\( \ \mathrm{M} \ \)とし、 辺\( \ \mathrm{AB} \ \)上に点\( \ \mathrm{C} \ \)を \( \ \mathrm{CM}\perp \mathrm{OB} \ \)となるようにとる。
なお\( \ \overrightarrow{\mathrm{OA}} = \vec{a} \ \)、 \( \ \overrightarrow{\mathrm{OB}} =\vec{b} \ \)とする。
(1) 内積の値\( \ \vec{a}\cdot \vec{b} \ \)を求めよ。
(2) 線分の長さの比\( \ \mathrm{AC}:\mathrm{CB} \ \)を最も簡単な整数の比で表せ。
(3) \( \ \angle \mathrm{AOB} \ \)の二等分線と辺\( \ \mathrm{AB} \ \), 線分\( \ \mathrm{CM} \ \)との交点をそれぞれ\( \ \mathrm{D} \ \)、\( \ \mathrm{E} \ \)とする。
このとき、 三角形\( \ \mathrm{CDE} \ \)と三角形\( \ \mathrm{OEM} \ \)の面積の比を最も簡単な整数比で表せ。
また、 辺\( \ \mathrm{OB} \ \)の中点を\( \ \mathrm{M} \ \)とし、 辺\( \ \mathrm{AB} \ \)上に点\( \ \mathrm{C} \ \)を \( \ \mathrm{CM}\perp \mathrm{OB} \ \)となるようにとる。
なお\( \ \overrightarrow{\mathrm{OA}} = \vec{a} \ \)、 \( \ \overrightarrow{\mathrm{OB}} =\vec{b} \ \)とする。
(1) 内積の値\( \ \vec{a}\cdot \vec{b} \ \)を求めよ。
(2) 線分の長さの比\( \ \mathrm{AC}:\mathrm{CB} \ \)を最も簡単な整数の比で表せ。
(3) \( \ \angle \mathrm{AOB} \ \)の二等分線と辺\( \ \mathrm{AB} \ \), 線分\( \ \mathrm{CM} \ \)との交点をそれぞれ\( \ \mathrm{D} \ \)、\( \ \mathrm{E} \ \)とする。
このとき、 三角形\( \ \mathrm{CDE} \ \)と三角形\( \ \mathrm{OEM} \ \)の面積の比を最も簡単な整数比で表せ。
解法
内積を求める
$$\begin{align}\cos \angle \mathrm{AOB}=&\frac{\vec{a}\cdot \vec{b}}{\vert \vec{a} \vert\vert \vec{b} \vert} \\\\ \cos 60^{\circ}=&\frac{\vec{a}\cdot \vec{b}}{3\times 4} \\\\ \frac{1}{2}=&\frac{\vec{a}\cdot \vec{a}}{12}\\\\ \vec{a}\cdot \vec{b}=&6 \end{align}$$内分比を求める
$$\begin{align}\mathrm{CM} \perp \mathrm{OB}& \ \rm{より} \\\\ \overrightarrow{\mathrm{CM}}\cdot \vec{b}=&0 \\\\ \left( \overrightarrow{\mathrm{OM}}-\overrightarrow{\mathrm{OC}}\right)\cdot \vec{b}=&0\\\\ \frac{1}{2}\vec{b}\cdot \vec{b}-\overrightarrow{\mathrm{OC}}\cdot \vec{b}=&0\\\\ \overrightarrow{\mathrm{OC}}\cdot \vec{b}=&8 \end{align}$$ ここで、\( \ \overrightarrow{\mathrm{OC}} \ \) は、線分\( \ \mathrm{AB} \ \)を\( \ \alpha:\left( 1-\alpha\right) \ \) に内分するものとする。（ただし、\( \ \alpha \ \) は\( \ 0 \lt \alpha \lt 1 \ \) を満たす実数）
\( \ \overrightarrow{\mathrm{OC}}=\left( 1-\alpha\right)\vec{a}+\alpha\vec{b} \ \) と表せる。
$$\begin{align}\overrightarrow{\mathrm{OC}}\cdot \vec{b}=&8\\\\ \lbrace \left( 1-\alpha\right)\vec{a}+\alpha\vec{b}\rbrace\vec{b}=&8 \\\\ 6\left( 1-\alpha\right)+16\alpha=&8 \\\\ 6-6\alpha+16\alpha=&8\\\\ 10\alpha=&2\\\\ \alpha=&\frac{1}{5}\\\\ \\\\ \mathrm{AC}:\mathrm{CB}=&1:4 \end{align}$$
面積比を求める
$$\begin{align}\triangle \mathrm{CDE}:\triangle \mathrm{OEM}=&\frac{1}{2}\mathrm{EC}\cdot \mathrm{ED}\sin \angle \mathrm{CED}: \frac{1}{2}\mathrm{MD}\cdot \mathrm{EO}\sin \angle \mathrm{MEO}\\\\ =&\mathrm{CE}\cdot \mathrm{ED}:\mathrm{EO}\cdot \mathrm{OM} \end{align}$$ ここで、\( \ \triangle \mathrm{OCD} \ \) において、\( \ \mathrm{CD}:\mathrm{DB} \ \)を求める。$$\begin{align}\mathrm{AC}:\mathrm{CB}=&\frac{1}{5}:\frac{4}{5} \\\\ \mathrm{AD}:\mathrm{DB}=&\frac{3}{7}:\frac{4}{7}\quad \rm{(}\mathrm{OD} \rm{は}\angle \mathrm{AOB}\rm{の二等分線より)}\\\\ \rm{それぞれの内分比を}&35\rm{倍すると}\\\\\mathrm{AC}:\mathrm{CB}=&7:28\\\\\mathrm{AD}:\mathrm{DB}=&15:20\\\\ \mathrm{AD}:\mathrm{CD}=&15:7 \ \rm{より}\\\\ \mathrm{CD}:\mathrm{DB}=&8:20=2:5 \end{align}$$ 三角形\( \ \mathrm{OCB} \ \)における内分比は以下の図の青い数字のとおり。
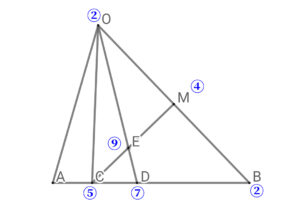線分の比を赤い文字で示す。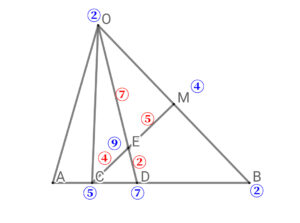
$$\begin{align}\triangle \mathrm{CDE}:\triangle \mathrm{OEM}=&\mathrm{CE}\cdot \mathrm{ED}:\mathrm{EO}\cdot \mathrm{OM}\\\\ =&2\times 4:5\times 7\\\\ =&8:35 \end{align}$$
こたえ
\( \ \vec{a}\cdot \vec{b}=6 \ \)\( \ \mathrm{AC}:\mathrm{CB}=1:4 \ \)
\( \ \triangle \mathrm{CDE}:\triangle \mathrm{OEM}=8:35 \ \)
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「平面ベクトルの内分比の活用」に関する問題を解いてみました。
問題
三角形\( \ \mathrm{OAB} \ \)があり、 \( \ \mathrm{OA}=3 \ \)、\( \ \mathrm{OB}=4 \ \)、\( \ \angle \mathrm{AOB}=60^{\circ} \ \) とする。
また、 辺\( \ \mathrm{OB} \ \)の中点を\( \ \mathrm{M} \ \)とし、 辺\( \ \mathrm{AB} \ \)上に点\( \ \mathrm{C} \ \)を \( \ \mathrm{CM}\perp \mathrm{OB} \ \)となるようにとる。
なお\( \ \overrightarrow{\mathrm{OA}} = \vec{a} \ \)、 \( \ \overrightarrow{\mathrm{OB}} =\vec{b} \ \)とする。
(1) 内積の値\( \ \vec{a}\cdot \vec{b} \ \)を求めよ。
(2) 線分の長さの比\( \ \mathrm{AC}:\mathrm{CB} \ \)を最も簡単な整数の比で表せ。
(3) \( \ \angle \mathrm{AOB} \ \)の二等分線と辺\( \ \mathrm{AB} \ \), 線分\( \ \mathrm{CM} \ \)との交点をそれぞれ\( \ \mathrm{D} \ \)、\( \ \mathrm{E} \ \)とする。
このとき、 三角形\( \ \mathrm{CDE} \ \)と三角形\( \ \mathrm{OEM} \ \)の面積の比を最も簡単な整数比で表せ。
また、 辺\( \ \mathrm{OB} \ \)の中点を\( \ \mathrm{M} \ \)とし、 辺\( \ \mathrm{AB} \ \)上に点\( \ \mathrm{C} \ \)を \( \ \mathrm{CM}\perp \mathrm{OB} \ \)となるようにとる。
なお\( \ \overrightarrow{\mathrm{OA}} = \vec{a} \ \)、 \( \ \overrightarrow{\mathrm{OB}} =\vec{b} \ \)とする。
(1) 内積の値\( \ \vec{a}\cdot \vec{b} \ \)を求めよ。
(2) 線分の長さの比\( \ \mathrm{AC}:\mathrm{CB} \ \)を最も簡単な整数の比で表せ。
(3) \( \ \angle \mathrm{AOB} \ \)の二等分線と辺\( \ \mathrm{AB} \ \), 線分\( \ \mathrm{CM} \ \)との交点をそれぞれ\( \ \mathrm{D} \ \)、\( \ \mathrm{E} \ \)とする。
このとき、 三角形\( \ \mathrm{CDE} \ \)と三角形\( \ \mathrm{OEM} \ \)の面積の比を最も簡単な整数比で表せ。
解法
内積を求める
$$\begin{align}\cos \angle \mathrm{AOB}=&\frac{\vec{a}\cdot \vec{b}}{\vert \vec{a} \vert\vert \vec{b} \vert} \\\\ \cos 60^{\circ}=&\frac{\vec{a}\cdot \vec{b}}{3\times 4} \\\\ \frac{1}{2}=&\frac{\vec{a}\cdot \vec{a}}{12}\\\\ \vec{a}\cdot \vec{b}=&6 \end{align}$$内分比を求める
$$\begin{align}\mathrm{CM} \perp \mathrm{OB}& \ \rm{より} \\\\ \overrightarrow{\mathrm{CM}}\cdot \vec{b}=&0 \\\\ \left( \overrightarrow{\mathrm{OM}}-\overrightarrow{\mathrm{OC}}\right)\cdot \vec{b}=&0\\\\ \frac{1}{2}\vec{b}\cdot \vec{b}-\overrightarrow{\mathrm{OC}}\cdot \vec{b}=&0\\\\ \overrightarrow{\mathrm{OC}}\cdot \vec{b}=&8 \end{align}$$ ここで、\( \ \overrightarrow{\mathrm{OC}} \ \) は、線分\( \ \mathrm{AB} \ \)を\( \ \alpha:\left( 1-\alpha\right) \ \) に内分するものとする。（ただし、\( \ \alpha \ \) は\( \ 0 \lt \alpha \lt 1 \ \) を満たす実数）
\( \ \overrightarrow{\mathrm{OC}}=\left( 1-\alpha\right)\vec{a}+\alpha\vec{b} \ \) と表せる。
$$\begin{align}\overrightarrow{\mathrm{OC}}\cdot \vec{b}=&8\\\\ \lbrace \left( 1-\alpha\right)\vec{a}+\alpha\vec{b}\rbrace\vec{b}=&8 \\\\ 6\left( 1-\alpha\right)+16\alpha=&8 \\\\ 6-6\alpha+16\alpha=&8\\\\ 10\alpha=&2\\\\ \alpha=&\frac{1}{5}\\\\ \\\\ \mathrm{AC}:\mathrm{CB}=&1:4 \end{align}$$
面積比を求める
$$\begin{align}\triangle \mathrm{CDE}:\triangle \mathrm{OEM}=&\frac{1}{2}\mathrm{EC}\cdot \mathrm{ED}\sin \angle \mathrm{CED}: \frac{1}{2}\mathrm{MD}\cdot \mathrm{EO}\sin \angle \mathrm{MEO}\\\\ =&\mathrm{CE}\cdot \mathrm{ED}:\mathrm{EO}\cdot \mathrm{OM} \end{align}$$ ここで、\( \ \triangle \mathrm{OCD} \ \) において、\( \ \mathrm{CD}:\mathrm{DB} \ \)を求める。$$\begin{align}\mathrm{AC}:\mathrm{CB}=&\frac{1}{5}:\frac{4}{5} \\\\ \mathrm{AD}:\mathrm{DB}=&\frac{3}{7}:\frac{4}{7}\quad \rm{(}\mathrm{OD} \rm{は}\angle \mathrm{AOB}\rm{の二等分線より)}\\\\ \rm{それぞれの内分比を}&35\rm{倍すると}\\\\\mathrm{AC}:\mathrm{CB}=&7:28\\\\\mathrm{AD}:\mathrm{DB}=&15:20\\\\ \mathrm{AD}:\mathrm{CD}=&15:7 \ \rm{より}\\\\ \mathrm{CD}:\mathrm{DB}=&8:20=2:5 \end{align}$$ 三角形\( \ \mathrm{OCB} \ \)における内分比は以下の図の青い数字のとおり。
線分の比を赤い文字で示す。$$\begin{align}\triangle \mathrm{CDE}:\triangle \mathrm{OEM}=&\mathrm{CE}\cdot \mathrm{ED}:\mathrm{EO}\cdot \mathrm{OM}\\\\ =&2\times 4:5\times 7\\\\ =&8:35 \end{align}$$
こたえ
\( \ \vec{a}\cdot \vec{b}=6 \ \)\( \ \mathrm{AC}:\mathrm{CB}=1:4 \ \)
\( \ \triangle \mathrm{CDE}:\triangle \mathrm{OEM}=8:35 \ \)
共有:
プロフィール
Author Profile
