高校数学の「正弦定理・余弦定理の活用」に関する問題を解いてみる。【Yahoo!知恵袋より】

読了時間: 約2分17秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「正弦定理・余弦定理の活用」に関する問題を解いてみました。
問題
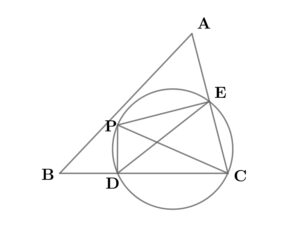
辺の長さ\( \ \mathrm{AB}=8 \ , \ \mathrm{BC}=7 \ , \ \mathrm{CA}=6 \ \)の三角形 \( \ \mathrm{ABC} \ \)においてこの三角形の内部の点 \( \ \mathrm{P} \ \) から辺\( \ \mathrm{BC} \ , \ \mathrm{CA} \ \)へ下ろした垂線の足をそれぞれ \( \ \mathrm{D} \ , \ \mathrm{E} \ \) としたとき、
\( \ \mathrm{PD} =2 \ , \ \mathrm{PE} =4 \ \)であったとする
問1 \( \ \mathrm{DE} \ \) の長さを求めよ。
問2 \( \ \mathrm{BC} \ \) の長さを求めよ。
\( \ \mathrm{PD} =2 \ , \ \mathrm{PE} =4 \ \)であったとする
問1 \( \ \mathrm{DE} \ \) の長さを求めよ。
問2 \( \ \mathrm{BC} \ \) の長さを求めよ。
解法
DEの長さ
三角形\( \ ABC \ \)において、余弦定理より$$\begin{align}\cos \angle \mathrm{ACB}=&\frac{\mathrm{BC}^2+\mathrm{CA}^2-\mathrm{AB}^2}{2\mathrm{BC}\cdot \mathrm{CA}} \\\\ =&\frac{7^2+6^2-8^2}{2\cdot 7\cdot 6} \\\\ =&\frac{1}{4} \end{align}$$ ここで、四角形\( \ \mathrm{PDCE} \ \)に外接する円を考える。
円に内接する四角形の性質より
\( \ \cos \angle \mathrm{EPD}=-\displaystyle\frac{1}{4} \ \)
三角形\( \ PDE \ \)において、余弦定理より
$$\begin{align}\cos \angle \mathrm{EPD}=&\frac{\mathrm{PD}^2+\mathrm{PE}^2-\mathrm{DE}^2}{2\mathrm{PD}\cdot \mathrm{PE}} \\\\ -\frac{1}{4}=&\frac{2^2+4^2-\mathrm{DE}^2}{2\cdot 2\cdot 4} \\\\ -4=&20-\mathrm{DE}^2\\\\ \mathrm{DE}^2=&24\\\\ \mathrm{DE} \gt& 0 \ \rm{より}\\\\ \mathrm{DE}=&2\sqrt{6} \end{align}$$
PCの長さ
\( \ \sin^{2} \theta+\cos^{2} \theta=1 \ \)より\( \ \sin \angle \mathrm{ECD}=\displaystyle\frac{\sqrt{15}}{4} \ \)
\( \ \angle \mathrm{PCD}=\angle \mathrm{R} \ \)より
\( \ \mathrm{PC} \ \)は三角形\( \ \mathrm{DCE} \ \)の外接円の直径である。
正弦定理より
$$\begin{align}2\mathrm{R}=&\frac{\mathrm{DE}}{\sin \angle \mathrm{ECD}} \\\\ =&2\sqrt{6}\times \frac{4}{\sqrt{15}} \\\\ =&\frac{8\sqrt{10}}{5} \end{align}$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません