そんなに値下げして大丈夫なの?!（数学が商魂をたくましくする）
読了時間: 約5分42秒
問題
焼きそばを1個\( \ 300 \ \)円で販売する。作る焼きそばの個数を\( \ x \ \)個とすると、焼きそばを作るのに必要な費用は表のようになる。
ただし、\( \ x \ \)は\( \ 300 \ \)以下の自然数である。
また、焼きそばの売り上げ金額から必要な費用を引いた金額を利益(単位は円)とし、作った焼きそばはすべて売り切れるとして考える。
焼きそばをすべて売り切るために最後の\( \ 30 \ \)個を1個あたり\( \ a \ \)円引きで販売することにした。
\( \ 151 \leqq x \leqq 300 \ \)のどの\( \ x \ \)に対しても値引きをしたときの利益が値引きをしなかったときの利益の半分以上であるように\( \ a \ \)の値を決める。
このとき、1個あたり最大何円値引きをすることができるか。ただし、値引きは\( \ 10 \ \)円単位とする。
| \( \ x \ \) | 焼きそば1個あたりの材料費と光熱費（変動費） | 機材のレンタル費（固定費） |
| \( \ 1 \leqq x \leqq 100 \ \) | 230円 | 1台必要で3000円 |
| \( \ 101 \leqq x \leqq 150 \ \) | 210円 | 1台必要で3000円 |
| \( \ 151 \leqq x \leqq 300 \ \) | 210円 | 2台必要で6000円 |
損益分岐点は2つの直線の交点
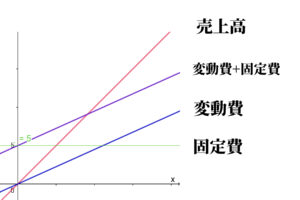損益分岐点は、売上高を表す赤い直線と、変動費+固定費を表す紫の直線の交点です。
売上数量を \( \ x \ \) ,金額を \( \ y \ \) とします。
販売単価を \( \ a \ \) , 一つあたりの変動費を \( \ b \ \) , 固定費を \( \ c \ \) とします。
売上高は \( \ y=ax \ \)
変動費は \( \ y=bx \ \)
固定費は \( \ y=c \ \)
変動費+固定費（費用）は \( \ y=bx+c \ \)
さらに、
損益分岐点の数量は、\( \ x=\displaystyle\frac{c}{\left( a-b\right)}=\displaystyle\frac{\rm{固定費}}{\left( \rm{販売単価}-\rm{変動費}\right)} \ \)
利益は、\( \ y=\left( a-b\right)x-c=\left( \rm{販売単価}-\rm{変動費}\right)x-\rm{固定費} \ \) で求められます。
解法
費用を決定する
問題より、\( \ 151 \ \)個以上販売することがわかっているので、変動費は\( \ 210 \ \)円/個、固定費は\( \ 6000 \ \)円となります。損益分岐点を求める
\( \ 151 \ \)個以上売ることにしたので、固定費がそれまでの倍かかることになりましたが、それでも利益は出るのでしょうか。（出なかったら、赤字になる）
そこで、損益分岐点を求めてみます。
売上高は、\( \ y=300x \ \)
費用は、\( \ y=210x+6000 \ \)です。
$$\begin{align}\rm{損益分岐点}:\rm{売上高}=&\rm{費用} \\\\ 300x=&210x+6000 \\\\ 90x=&6000\\\\ x=&66.6\cdots \end{align}$$ すなわち、\( \ 67 \ \)個以上販売すれば、確実に利益が生じるということになります。
機材を2台借りても無謀ではないということがわかり、ほっとひと安心です。
薄利多売でも利益を出すには
求めたいのは、\( \ 151 \ \)個から\( \ 300 \ \)個までの最大\( \ 150 \ \)個全てを\( \ a \ \)円引きで売ったとしても、\( \ 120 \ \)個は通常価格（\( \ 300 \ \)円）で売り、残り\( \ 30 \ \)個を\( \ a \ \)円引きで売ったときの利益の半分以上が出るような値引き額です。
以下の表は、販売数量の最大値\( \ x=300 \ \)のときの販売単価と費用についてまとめたものです。
| 販売単価 | 費用 | |||
| \( \ 150 \ \)個 | \( \ 120 \ \)個 | \( \ 30 \ \)個 | ||
| （\( \ 151 \ \)個以降）全て値引き | \( \ 300 \ \)円 | \( \ 300-a \ \)円 | \( \ 300-a \ \)円 | \( \ 69000 \ \)円 |
| （\( \ 151 \ \)個以降）\( \ 30 \ \)個は値引き | \( \ 300 \ \)円 | \( \ 300 \ \)円 | \( \ 300-a \ \)円 | \( \ 69000 \ \)円 |
\( \ 151 \ \)個以降\( \ 30 \ \)個だけ値引きの場合の売上高を\( \ \mathrm{U}_2 \ \),利益を\( \ \mathrm{P}_2 \ \) とします。
また、費用は\( \ \mathrm{C} \ \)とします。
$$\begin{align}\mathrm{P}_1=&\mathrm{U}_1-\mathrm{C} \\\\ =&300\times 150+\left( 300-a\right)\times 120+\left( 300-a\right)\times 30-\left( 210\times 300+6000\right) \\\\ =&45000+\left( 300-a\right)\times 150-69000\\\\ =&21000-150a \end{align}$$
$$\begin{align}\mathrm{P}_2=&\mathrm{U}_2-\mathrm{C} \\\\ =&300\times 150+300\times 120+\left( 300-a\right)\times 30-\left( 210\times 300+6000\right) \\\\ =&45000+36000+\left( 300-a\right)\times 30-69000\\\\ =&21000-30a \end{align}$$
$$\begin{align}\mathrm{P}_1 \geqq &\frac{1}{2}\mathrm{P}_2 \\\\ 2\mathrm{P}_1 \geqq &\mathrm{P}_2 \\\\ 2\left( 21000-150a\right) \geqq &21000-30a\\\\ 21000 \geqq &300a-30a\\\\ 21000 \geqq &270a\\\\ 77.7\cdots \geqq &a \end{align}$$
すなわち、\( \ 78 \ \)円未満の値引き額なら、目標は達成できるわけです。
しかし、値引き額は\( \ 10 \ \)円単位となっていますので、
求める最大の値引き額は、\( \ a=70 \ \)となります。
検算してみる
\( \ a=70 \ \)を\( \ \mathrm{P}_1 \ \),\( \ \mathrm{P}_2 \ \)に代入してみます。$$\begin{align}\frac{\mathrm{P}_1}{\mathrm{P}_2}=&\frac{21000-150\times 70}{21000-30\times 70} \\\\ =&\frac{10500}{18900} \\\\ =&0.556 \gt 0.5 \end{align}$$
ちなみに、\( \ a=80 \ \)なら、
\( \ \displaystyle\frac{\mathrm{P}_1}{\mathrm{P}_2}=\frac{9000}{18600} \fallingdotseq 0.484 \lt 0.500 \ \)
となり、利益は出ますが、目標は達成できないことになります。
「最終御礼!! 通常価格300円のところ、150個限定 230円!!」なんてポップが出ていたら、
お客さんは飛びついちゃうでしょうね。
でも、売る側からすると、一応利益は出ますので、ふところは傷まないし、
なんなら、行列ができてぽんぽん売れるので、見ていても（売っていても）楽しいはずです。
お客さんは飛びついちゃうでしょうね。
でも、売る側からすると、一応利益は出ますので、ふところは傷まないし、
なんなら、行列ができてぽんぽん売れるので、見ていても（売っていても）楽しいはずです。
よろしければ,アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『そんなに値下げして大丈夫なの?!』です。
共有:
プロフィール
Author Profile