弧と弦に囲まれた部分の面積を求める

読了時間: 約2分39秒
インスタグラムのハッシュタグ数学で問題が流れてきたので、解いてみました。
問題
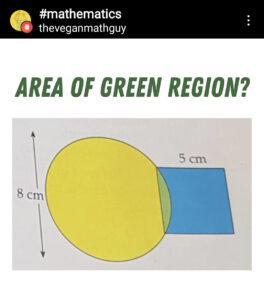 直径8cmの円と一辺5cmの正方形が、正方形の一辺が円の弦となるように交わっているとき、
直径8cmの円と一辺5cmの正方形が、正方形の一辺が円の弦となるように交わっているとき、弦と弧で囲まれた部分の面積はいくらか。という問題です。
方針
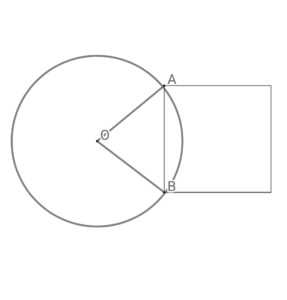 GeoGebraで描き直してみました。
GeoGebraで描き直してみました。
方針としては、扇形AOBから三角形AOBを引いて求めようと思います。
特に\( \ \angle \mathrm{AOB}=\theta^{\circ} \ \),\( \ \pi=3.14 \ \)とします。
解法
求める面積を\( \ \mathrm{S} \ \)とする。$$\begin{align}\mathrm{S}=&4^2\pi\times \frac{\theta}{360}-\frac{1}{2}\times 4^2\sin \theta \\\\ =&\frac{4}{90}\pi\theta-8\sin \theta \end{align}$$
ここで、\( \ \triangle \mathrm{AOB} \ \)において余弦定理より
$$\begin{align}\cos \theta=&\frac{4^2+4^2-5^2}{2\times 4\times 4} \\\\ =&\frac{32-25}{32} \\\\ =&\frac{7}{32} \end{align}$$
また、\( \ \sin^{2} \theta+\cos^{2} \theta=1 \ \) より
$$\begin{align}\sin^{2} \theta=&1-\cos^{2} \theta \\\\ =&1-\left( \frac{7}{32}\right)^2 \\\\ =&\frac{975}{32^2}\\\\ \theta&{\rm{は鋭角なので}}\\\\ \sin \theta=&\frac{5\sqrt{39}}{32} \end{align}$$
あらためて
$$\begin{align}\mathrm{S}=&\frac{4}{90}\pi\theta-8\sin \theta \\\\ =&\frac{4}{90}\pi\cos^{-1} \theta-8\times \frac{5\sqrt{39}}{32} \\\\ \cos^{-1} \theta \fallingdotseq &77.4^{\circ} \ {\rm{より}}\\\\ =&\frac{4}{90}\times 3.14\times 77.4-\frac{5\sqrt{39}}{4}\\\\ =&10.8-7.8\\\\ =&3 \end{align}$$
逆三角関数ってのがあるんですね
解法の方針を立てたまでは問題なかったのですが、\( \ \theta \ \)の値、すなわち、\( \ \theta \ \) は何度なのかを求める知識を持ち合わせていませんでした。そこで、Googleさんに、「コサインから角度を求める」と入力して検索したところ、
「逆三角関数」というのがあることを知りました。
関数電卓を使って求める方法を知り、スマホに入れている関数電卓アプリで求めました。

まずは、角度もコサインの値も知っている\( \ 60^{\circ} \ \) で実験して
入力方法に間違いがないことを確かめて、
その後、\( \ \cos^{-1} \theta \ \)を求め、
念押しとして、\( \ \sin^{-1} \theta \ \)も求めて、角度を確定しました。
入力方法に間違いがないことを確かめて、
その後、\( \ \cos^{-1} \theta \ \)を求め、
念押しとして、\( \ \sin^{-1} \theta \ \)も求めて、角度を確定しました。
\( \ \sin^{-1} \theta \ \) のことを\( \ \arcsin\theta \ \)(アークサインシータ)と呼ぶんだそうです。

軽い気持ちで、問題を解いたのに、思いがけず逆三角関数を知ることができて、ラッキーでした。
こたえ
3








