平面ベクトル三角形の内分比を統一する（その5）【たすきがけで比を統一せよ!!】

2023年1月10日ベクトル実用数学技能検定（数学検定数検),数検2級,数検準1級

読了時間: 約5分58秒

問題

$\triangle \mathrm{OAB}$があり,辺 $\mathrm{OA}$を $2:1$に内分する点を$\mathrm{C}$,
辺$\mathrm{AB}$を$2:1$に内分する点を$\mathrm{D}$とする.
また,$\overrightarrow{\mathrm{OA}}=\overrightarrow{a}, \ \overrightarrow{\mathrm{OB}}=\overrightarrow{b}$とする.

(1) $\overrightarrow{\mathrm{OC}}$を$\overrightarrow{a}$を用いて表せ.また,$\overrightarrow{\mathrm{OD}}$を$\overrightarrow{a} \ , \ \overrightarrow{b}$を用いて表せ.
(2)　$s$は実数とし,直線$\mathrm{CD}$上に$\overrightarrow{\mathrm{CE}}=s\overrightarrow{\mathrm{CD}}$となるような点$\mathrm{E}$をとる.
$\overrightarrow{\mathrm{OE}}$を$s \ , \ \overrightarrow{a} \ , \ \overrightarrow{b}$を用いて表せ.また,$\mathrm{E}$が直線$\mathrm{OB}$上にあるとき,$s$の値を求めよ.
(3)　（2)の点$\mathrm{E}$が直線$\mathrm{OB}$上にあり,$\mathrm{OA}=2, \ $$\mathrm{OB}=3, \ $$\angle \mathrm{AOB}=90^{\circ}$であるとする.また,$t$は実数とし,直線$\mathrm{AB}$上に$\overrightarrow{\mathrm{AF}}=t\overrightarrow{\mathrm{AB}} \ \left( t \neq 0\right)$となるような点$\mathrm{F}$をとる.$\mathrm{EA}=\mathrm{EF}$であるとき,$ \ t$の値を求めよ.

(1)を解く。

Lukia

内分比を統一することにずいぶん慣れてきていると思うので、
今回からは、統一された図を示すことにします。
ただし、今回はあんまり統一する必要もないんですけどね。

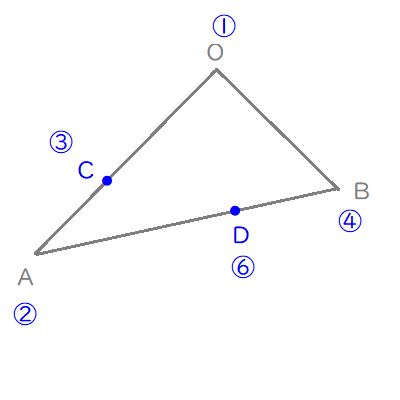
$$\begin{align}\overrightarrow{\mathrm{OC}}=&\displaystyle\frac{2}{3}\overrightarrow{a} \\\\ \overrightarrow{\mathrm{OD}}=&\displaystyle\frac{1}{3}\left( \overrightarrow{a}+2\overrightarrow{b}\right) \end{align}$$

(2)を解く。

$$\begin{align}\overrightarrow{\mathrm{CE}}=&s\overrightarrow{\mathrm{CD}} \\\\ \overrightarrow{\mathrm{OE}}=&\left( 1-s\right)\overrightarrow{\mathrm{OC}}+s\overrightarrow{\mathrm{OD}} \\\\ =&\displaystyle\frac{2}{3}\left( 1-s\right)\overrightarrow{a}+\displaystyle\frac{1}{3}s\left( \overrightarrow{a}+2\overrightarrow{b}\right)\\\\ =&\displaystyle\frac{1}{3}\left( 2-s\right)\overrightarrow{a}+\displaystyle\frac{2}{3}s\overrightarrow{b} \end{align}$$

$$\begin{align}点\mathrm{E}が&直線\mathrm{OB}上にあるということは \\\\ \overrightarrow{\mathrm{OE}}=&k\overrightarrow{\mathrm{OB}}\quad \left( k \ は実数\right) \quad であるから,\\\\ \displaystyle\frac{1}{3}\left( 2-s\right)=&0\\\\ すなわち \ &s=2 \end{align}$$

(3)を解く。

Lukia

(2)で、$ \ s=2 \ $とわかりましたので、
$ \ k=\displaystyle\frac{4}{3} \ $となり、図は以下のように描き換えられます。
また、$ \ \angle \mathrm{AOB}=90^{\circ} \ $ということから、ベクトルの内積$ \ \overrightarrow{a}\cdot \overrightarrow{b}=0 \ $ということもわかりますね。

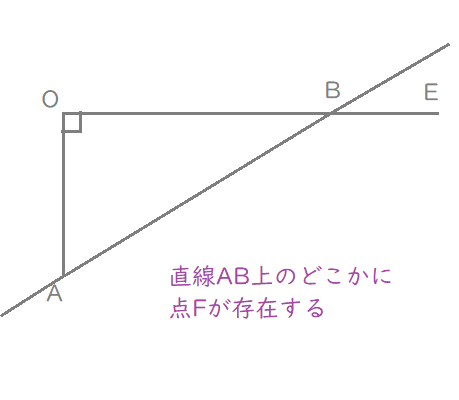
$$\begin{align}\left( 2\right)の&s=2 \ より \\\\ \overrightarrow{\mathrm{OE}}=&\displaystyle\frac{4}{3}\overrightarrow{b} \ である. \\\\ また, \ &\angle \mathrm{AOB}=90^{\circ} \ より,\\\\ \overrightarrow{a}\cdot \overrightarrow{b}=&0 \ である. \end{align}$$

$$\begin{align}\overrightarrow{\mathrm{AF}}=&t\overrightarrow{\mathrm{AB}} \ より,\\\\ \overrightarrow{\mathrm{OF}}=&-\left( t+1\right)\overrightarrow{a}+t\overrightarrow{b} \end{align}$$
$$\begin{align}\overrightarrow{\mathrm{EA}}=&\overrightarrow{a}-\displaystyle\frac{4}{3}\overrightarrow{b} \\\\ \overrightarrow{\mathrm{EF}}=&-\left( t+1\right)\overrightarrow{a}+\left( t-\displaystyle\frac{4}{3}\right)\overrightarrow{b} \\\\ \\\\ \vert \overrightarrow{\mathrm{EA}} \vert^2=&\vert \overrightarrow{\mathrm{EF}} \vert^2 \\\\ 4-2\cdot \left( -\displaystyle\frac{4}{3}\right)\overrightarrow{a}\cdot \overrightarrow{b}+\displaystyle\frac{16}{9}\cdot 9=&\left( t+1\right)^2\cdot 4-2\cdot \left( -t-1\right)\left( t-\displaystyle\frac{4}{3}\right)\overrightarrow{a}\cdot \overrightarrow{b}+\left( t-\displaystyle\frac{4}{3}\right)^2\cdot 9\\\\ 20=&13t^2-16t+20\\\\ 13t^2-16t=&0\\\\ t \neq &0\quad より,\\\\ t=&\displaystyle\frac{16}{13} \end{align}$$

こたえ

$$\begin{align}\left( 1\right)\quad &\overrightarrow{\mathrm{OC}}=\displaystyle\frac{2}{3}\overrightarrow{a} \\\\ &\overrightarrow{\mathrm{OD}}=\displaystyle\frac{1}{3}\left( \overrightarrow{a}+2\overrightarrow{b}\right) \\\\ \left( 2\right)\quad &\overrightarrow{\mathrm{OE}}=\displaystyle\frac{1}{3}\left( 2-s\right)\overrightarrow{a}+\displaystyle\frac{2}{3}s\overrightarrow{b}\\\\ &s=2 \\\\ \left( 3\right)\quad &t=\displaystyle\frac{16}{13} \end{align}$$