【 41 / 42 】 論理と集合 「必要条件と十分条件の判定問題」を解いてみる。　

主語(N:必要)は、「 \( \ \triangle \mathrm{ABC} \ \)において\( \ \mathrm{AB}^2+\mathrm{BC}^2=\mathrm{CA}^2 \ \)である 」です。

これは、ピタゴラスの「三平方の定理」のことですね。
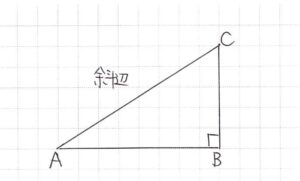
斜辺（直角の対辺）の二乗は、直角を挟む辺の二乗の和に等しい。

この場合、\( \ \triangle \mathrm{ABC} \ \)は、
\( \ \mathrm{AC} \ \)が斜辺、\( \ \mathrm{AB}\perp\mathrm{BC} \ \)の直角三角形だとわかります。
ゆえに、「 \( \ \triangle \mathrm{ABC} \ \)は\( \ \angle \mathrm{B}=90^{\circ} \ \)の直角三角形」だといえます。

国語的には、厳密な述語は「○○条件である」の部分ですが、
この述語を修飾（詳しく説明）する「 \( \ \triangle \mathrm{ABC} \ \)が\( \ \angle \mathrm{B}=90^{\circ} \ \)の直角三角形である（ための） 」を
述語(S:十分）としておきます。

主語(N:必要）から「 \( \ \triangle \mathrm{ABC} \ \)は\( \ \angle \mathrm{B}=90^{\circ} \ \)の直角三角形」が導かれ、
これは、述語(S:十分）と同義です。

ゆえに数学的には、
主語(N:必要）\( \ =\ \) 述語(S:十分）と表せます。

よって、答えは、「 （ア）　必要十分条件である 」 となります。