中学数学の食塩水融合問題(その2)

読了時間: 約4分18秒
[mathjax]

Lukia
今回の問題は、「とりだし」問題と「2種類の濃度の食塩水を混ぜ合わせる」問題の融合問題です。
問題
質量パーセント濃度が16%の食塩水と8%の食塩水を混ぜて、ある濃度の食塩水を作ろうとしたところ、
分量を逆にしたため、濃度が11%の食塩水が400gできてしまった。
本来、作ろうとした食塩水の濃度は何%であったか。
分量を逆にしたため、濃度が11%の食塩水が400gできてしまった。
本来、作ろうとした食塩水の濃度は何%であったか。
16%の食塩水は何gあるのか。

もも
この問題、「取り出して」という言葉がありますから、「とりだし」問題だとはわかりますが、
でも1回目の操作は、食塩水を100g取り出して、100gの水を加えているのに、
2回目は、食塩水を200g取り出して、200gの水を加えてます。
前回まで使ってきた「公式」はそのままでは使えませんね。
でも1回目の操作は、食塩水を100g取り出して、100gの水を加えているのに、
2回目は、食塩水を200g取り出して、200gの水を加えてます。
前回まで使ってきた「公式」はそのままでは使えませんね。

Lukia
そうですね。簡単に累乗にはできませんから、「公式」を書き直したほうがいいかもしれませんね。

もも
それもありますが、16%の食塩水がはじめ何gあったかもわからないじゃないですか!
文字を2つおかなきゃいけないのかなぁ。
文字を2つおかなきゃいけないのかなぁ。

Lukia
この場合、ある条件さえ守れば、16%の食塩水のはじめの重さは、
解答するわたしたちが自由に設定してもかまわないんですよ。
解答するわたしたちが自由に設定してもかまわないんですよ。

もも
えっ、そうなんですか?

Lukia
はい。だって、1000gだろうと、300gだろうと、濃度は16%で一定なわけでしょ?
式を立てながら、計算しやすそうな「はじめの重さ」を設定すればいいわけです。
式を立てながら、計算しやすそうな「はじめの重さ」を設定すればいいわけです。

もも
なるほど~。

Lukia
文字でおくつもりだったなら、数字でおいてもかまいませんよね。
しかし、数字でおく場合は、条件がありますよね。
取り出す食塩水の重さから考えると、
もとの食塩水は、「整数値」で最低何g以上あればよいですか?
しかし、数字でおく場合は、条件がありますよね。
取り出す食塩水の重さから考えると、
もとの食塩水は、「整数値」で最低何g以上あればよいですか?

もも
一回目は、100g取り出して、
二回目は、200g取り出した・・・
はっ!取り出して、マイナスになることはありえないから、200g以上ですか?
二回目は、200g取り出した・・・
はっ!取り出して、マイナスになることはありえないから、200g以上ですか?

Lukia
惜しいっ!
もし、もともと200gだったら、二回目の操作で、食塩水が入っていた器は空っぽになってしまいます。
食塩水が存在しないのですから、ただの水が入ることになってしまいますよ?
ということは、6行目にある「この食塩水を」というのは、表現がおかしいことになってしまいますよね。
もし、もともと200gだったら、二回目の操作で、食塩水が入っていた器は空っぽになってしまいます。
食塩水が存在しないのですから、ただの水が入ることになってしまいますよ?
ということは、6行目にある「この食塩水を」というのは、表現がおかしいことになってしまいますよね。

Lukia
この「食塩水問題シリーズ」では、水に食塩水が含まれていないことをイメージしてもらうために、わざと「0%食塩水」なんて表現していましたが、
本来はそんな表現しませんからね。
ということは、たしかに「整数値」だけれど、200gではまずいわけです。
本来はそんな表現しませんからね。
ということは、たしかに「整数値」だけれど、200gではまずいわけです。

もも
なるほど。
じゃ、200g取り出しても、わずかでも残っていればいいのだから、
201g以上ですか?
じゃ、200g取り出しても、わずかでも残っていればいいのだから、
201g以上ですか?

Lukia
そうですね。今回は、「整数」と限定したので201g以上ですが、
本来は、200.0001gなどでも、条件を満たしていることになりますね。
本来は、200.0001gなどでも、条件を満たしていることになりますね。

もも
まぁでも、200.0001gなんてめんどくさいですね。(笑)

Lukia
実際解いてみると、 400gが解きやすかったので、
16%の食塩水は、400gあると仮定しましょう。
16%の食塩水は、400gあると仮定しましょう。
公式を書き直して、食塩水の濃度を求める。

Lukia
これまでは、回数によって、取り出す食塩水の重さや混ぜる水の重さに違いはありませんでしたから、
以下の公式でよかったのですが、

今回は、一回目と二回目で、重さが異なるので、公式をちょっと書き変えねばなりませんね。
以下の公式でよかったのですが、
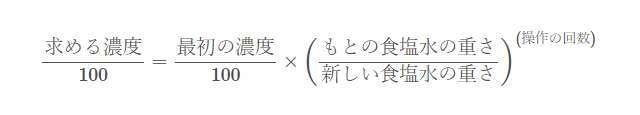
今回は、一回目と二回目で、重さが異なるので、公式をちょっと書き変えねばなりませんね。

もも
そうですよねぇ。

Lukia
ももちゃん、
ちょっと質問なのですが、
\(\Large a^2\) を別の表現ができませんか?
ちょっと質問なのですが、
\(\Large a^2\) を別の表現ができませんか?

もも
別の表現?
\(\Large a^2=a\times a\) です。
\(\Large a^2=a\times a\) です。

Lukia
では、逆に、
\(\Large a\times b\times b\times a\times a\) なら?
\(\Large a\times b\times b\times a\times a\) なら?

もも
$$\Large a\times b\times b\times a\times a=a^3b^2$$
ですね。

もも
あっ、つまり、一回目と二回目の操作で扱う重さが違うわけだから、
累乗じゃなくて、かけ算になるんだ!
累乗じゃなくて、かけ算になるんだ!

Lukia
そうです。
カンがいいですね。
カンがいいですね。


Lukia
今回は、2つの操作を行うので、カッコは2つ書いていますが、
もし、3回目に300g取り出して、水を300g加えた。となったら、
カッコを3つに増やすことになります。
もし、3回目に300g取り出して、水を300g加えた。となったら、
カッコを3つに増やすことになります。

もも
なるほど。
でも、「公式」の形としては、最初に覚えたものとそんなに変わらないんですね。
でも、「公式」の形としては、最初に覚えたものとそんなに変わらないんですね。

Lukia
そのとおりです。
それでは、新しい「公式」をもとに、式を立てていきましょう。
それでは、新しい「公式」をもとに、式を立てていきましょう。
1行目から5行目の式を立てて、計算する。

Lukia

を参考に式を立てていきます。
$$\Large 16%の食塩水が400gあると仮定し、$$
$$\Large できあがる食塩水の濃度をx %とする。$$
$$\Large \frac{x}{100}=\frac{16}{100}\times \frac{300}{400}\times \frac{200}{400}$$
$$\Large \frac{x}{100}=\frac{16}{100}\times \frac{3\times 2}{4\times 4}$$
$$\Large \frac{x}{100}=\frac{6}{100}$$
$$\Large x=6$$

Lukia
16%の食塩水400gは、二回の操作で、
6%の食塩水400gになりました。
6%の食塩水400gになりました。
2種類の濃度の食塩水を混ぜ合わせる。

もも
6行目から9行目まではこれまでやってきた、表を描いて解く問題ですね。

Lukia
そうですね。
ももちゃん、ふきだしの外に式を立てて、計算してみてくれませんか。
ももちゃん、ふきだしの外に式を立てて、計算してみてくれませんか。

もも
は~い、やってみます!


もも
取り出した食塩水の重さは、 \(\Large 200\) gです。

Lukia
表を描かずにやってましたね。

もも
はい。もう慣れて、頭の中で描きながら式が立てられました。
こたえ
200g[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません