補助線を使って、三平方の定理に持ち込む【粗忽な大人、高校入試問題を解く〜それ、誤答です!〜】

深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。
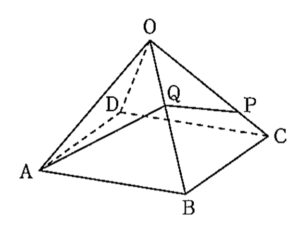 上の図のように、底面が、1辺の長さが \( \ 4 \ \)cm の正方形\( \ \mathrm{ABCD} \ \)で、\( \ \mathrm{OA}=\mathrm{OB}=\mathrm{OC}=\mathrm{OD}=4 \ \)cmの正四角すいがある。辺\( \ \mathrm{OC} \ \)上に、\( \ \mathrm{OP}=3 \ \)cmとなるように点\( \ \mathrm{P} \ \)をとる。辺\( \ \mathrm{OB} \ \)上に点\( \ \mathrm{Q} \ \)をとり、\( \ \mathrm{AQ}+\mathrm{QP} \ \)が最小となるようにするとき、\( \ \mathrm{AQ}+\mathrm{QP} \ \)は何cmか。
上の図のように、底面が、1辺の長さが \( \ 4 \ \)cm の正方形\( \ \mathrm{ABCD} \ \)で、\( \ \mathrm{OA}=\mathrm{OB}=\mathrm{OC}=\mathrm{OD}=4 \ \)cmの正四角すいがある。辺\( \ \mathrm{OC} \ \)上に、\( \ \mathrm{OP}=3 \ \)cmとなるように点\( \ \mathrm{P} \ \)をとる。辺\( \ \mathrm{OB} \ \)上に点\( \ \mathrm{Q} \ \)をとり、\( \ \mathrm{AQ}+\mathrm{QP} \ \)が最小となるようにするとき、\( \ \mathrm{AQ}+\mathrm{QP} \ \)は何cmか。2022年大問2-(2)
中学生で余弦定理?!
2つの辺の和の最小値は、線分\( \ \mathrm{AP} \ \)上に中継点である点\( \ \mathrm{Q} \ \)があること。2点間の距離は、三平方の定理を用いれば求められることがわかります。

もともと幾何の問題は苦手なので、悩んでしまいました。
条件を図におこしてみると、これは余弦定理を使うしかないような状況です。

回答者のアドバイスは、「補助線を使って、三平方の定理に持ち込む」。

解法
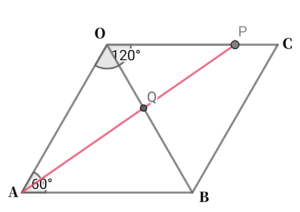 \( \ \mathrm{AQ}+\mathrm{QP} \ \)が最小となるのは、
\( \ \mathrm{AQ}+\mathrm{QP} \ \)が最小となるのは、
線分\( \ \mathrm{AP} \ \)上に点\( \ \mathrm{Q} \ \)が存在するとき。
半直線\( \ \mathrm{AO} \ \)に対し、点\( \ \mathrm{P} \ \)から垂線をおろし、その交点を\( \ h \ \)とする。
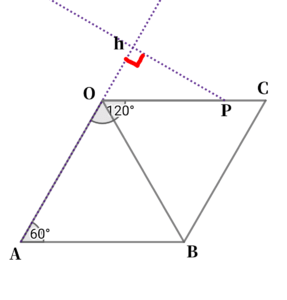
\( \ \triangle \mathrm{OP}h \ \)は、\( \ \angle h \mathrm{OP}=60^{\circ} \ \),\( \ \angle \mathrm{OP}h=30^{\circ} \ \)の直角三角形であるから、
辺\( \ \mathrm{O}h=\displaystyle\frac{3}{2} \ \)cm,
辺\( \ h\mathrm{P}=\displaystyle\frac{3}{2}\sqrt{3} \ \)cmである。
以上より、\( \ \triangle \mathrm{A}h\mathrm{P} \ \)も\( \ \angle \mathrm{A}h\mathrm{P}=90^{\circ} \ \)の直角三角形である。
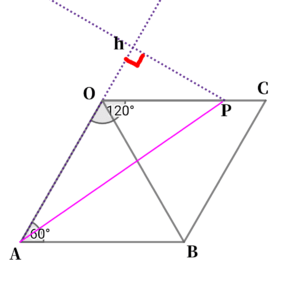 三平方の定理より、
三平方の定理より、
$$\begin{align}\mathrm{AP}^2=&\mathrm{A}h^2+h\mathrm{P}^2 \\\\ =&\left( 4+\frac{3}{2}\right)^2+\left( \frac{3}{2}\sqrt{3}\right)^2 \\\\ =&16+12+\frac{9}{4}+\frac{9}{4}\times 3\\\\ =&28+\frac{9}{4}\left( 1+3\right)\\\\ =&37 \end{align}$$
\( \ \mathrm{AP} \gt 0 \ \)より
\( \ \mathrm{AP}=\sqrt{37} \ \)
こたえ
\( \ \mathrm{AP}=\sqrt{37} \ \)
余弦定理でも解いてみる
\( \ \triangle \mathrm{OAP} \ \)において余弦定理より$$\begin{align}\cos \angle \mathrm{AOP}=&\frac{\mathrm{OA}^2+\mathrm{OP}^2-\mathrm{AP}^2}{2\mathrm{OA}\times \mathrm{OP}} \\\\ \cos 120^{\circ}=&\frac{16+9-\mathrm{AP}^2}{2\cdot 4\cdot 3} \\\\ -\frac{1}{2}=&\frac{25-\mathrm{AP}^2}{2\cdot 4\cdot 3} \\\\ -12=&25-\mathrm{AP}^2\\\\ \mathrm{AP}^2=&37\\\\ \mathrm{AP} \gt &0\quad より\\\\ \mathrm{AP}=&\sqrt{37}\end{align}$$
粗忽な大人、高校入試問題を解く〜それ、誤答です!〜の記事一覧
[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません