定額貯金と複利（その1）【大学入学共通テスト2023年数学ⅡB】

2023年1月31日大学入学共通テスト,数列

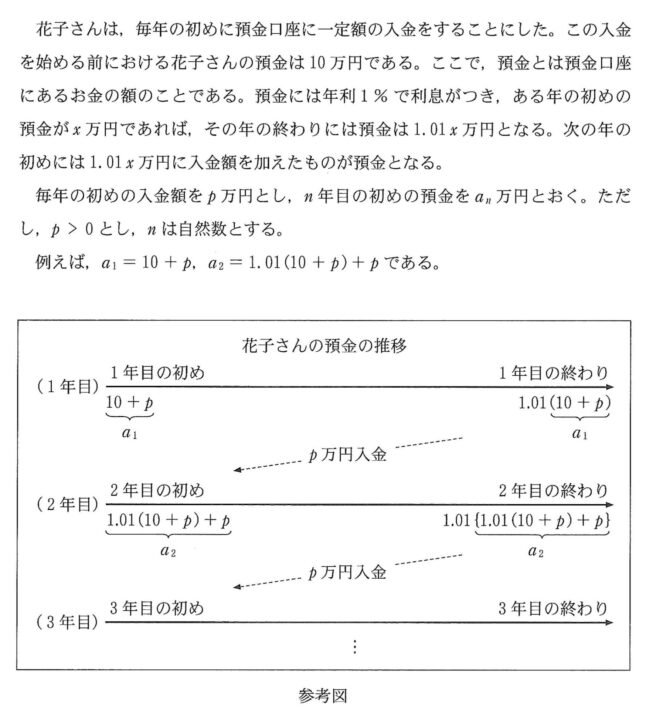\( \ a_2=1.01\times a_1+p \ \) より
$$\begin{align}a_3=&1.01\times a_2+p \\\\ =&{\color{#0004fc}{1.01\lbrace 1.01\left( 10+p\right)+p\rbrace+p}} \end{align}$$
すべての自然数 \( \ n \ \) について
\( \ a_{n+1}={\color{#0004fc}{1.01}}a_n+{\color{#0004fc}{p}} \ \) が成り立つ。
$$\begin{align}a_{n+1}=&1.01a_n+p \\\\ \left( a_{n+1}-\alpha\right)=&1.01\left( a_n-\alpha\right) \\\\ -1.01\alpha+\alpha=&p\\\\ 0.01\alpha=&-p\\\\ \alpha=&-100p\\\\ \left( a_{n+1}+{\color{#0004fc}{100}}p\right)=&{\color{#0004fc}{1.01}}\left( a_n+100p\right) \end{align}$$

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2023年数学ⅡBの記事一覧

2023年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。